Edutafsi.com - Contoh Soal Momen Inersia. Momen inersia (I) merupakan kelembaman rotasi yaitu kecenderungan benda untuk mempertahankan kedudukannya sehingga tidak berotasi. Momen inersia analog dengan massa sebagai kelembaman translasi. Sebenarnya, untuk mempermudah mempelajari tentang momen inersia ataupun momen gaya, kita dapat melihat perbandingan antara dinamika translasi dan Rotasi. Anda dapat membaca artikel hubungan keduanya untuk melihat bagaimana hubungan antara besaran-besaran dalam gerak translasi dan gerak rotasi. Jika anda menguasai konsep gerak translasi, maka gerak rotasi tidak akan sulit anda pahami.
Dengan :
I = momen inersia (kg m2)
Besarnya momen inersia yang dimiliki oleh benda bergantung kepada beberapa faktor yaitu :
1). Massa benda
2). Bentuk benda
3). Letak sumbu putar
4). Jarak ke sumbu putar.
Contoh 1 : Momen Inersia Sistem Partikel
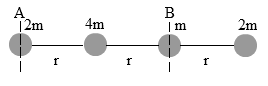
Empat buah partikel dihubungkan oleh sebuah batang yang massanya diabaikan, ditunjukkan seperti gambar di bawah ini. Tentukan momen inersia sistem partikel bila :
Pembahasan :
Contoh 2 : Momen Inersia batang Homogen
Dengan menggunakan rumus pergeseran poros, buktikanlah bahwa momen inersia batang homogen yang diputar pada salah satu ujungnya dapat dihitung dengan rumus I = ⅓ m.l 2.
Pembahasan :
Saat poros bergeser ke salah satu ujung artinya poros digeser sejauh ½l dari pusat, sehingga :
I = 1⁄12 m.l2 + m.(k.l)2
⇒ I = 1⁄12 m.l2 + m.(½.l)2
⇒ I = 1⁄12 m.l2 + ¼ m.l2
⇒ I = (1⁄12 + ¼) m.l2
⇒ I = (1⁄12 + 3⁄12) m.l2
⇒ I = (4⁄12) m.l2
⇒ I = 1⁄3 m.l2 (Terbukti).
Contoh 3 : Momen Inersia Melalui Pusat Batang
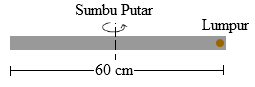
Diketahui sebuah batang homogen bermassa 0,6 kg dan panjang 60 cm. Jika gumpalan lumpur bermassa 20 gram dilempar dan menempel pada salah satu ujung batang, maka momen inersia sistem melalui pusat batang adalah ....
A. 1,89 x 10-2 kg m2
B. 1,98 x 10-2 kg m2
C. 2,18 x 10-2 kg m2
D. 2,48 x 10-2 kg m2
E. 2,98 x 10-2 kg m2
Pembahasan :
I = I batang + I lumpur
⇒ I = 1⁄12 m.l2 + mR2
⇒ I = 1⁄12 (0,6).(0,6)2 + 0,02 (0,3)2
⇒ I = 0,018 + 0,0018
⇒ I = 0,0198
⇒ I = 1,98 x 10-2 kg m2
A. 1,05 x 10-2 kg m2
B. 1,25 x 10-2 kg m2
C. 1,05 x 10-3 kg m2
D. 1,45 x 10-3 kg m2
E. 1,05 x 10-4 kg m2
Rumus Umum Momen Inersia
Momen inersia merupakan hasil kali antara massa dengan kuadrat jarak massa terhadap titik porosnya. Atau secara matematis dapat dihitung dengan menggunakan rumus berikut ini :| I = ∑m.R2 |
| I = m1.R12 + m2.R22 + ..... + mn.Rn2 |
Dengan :
I = momen inersia (kg m2)
R = jarak ke titik poros (m)
m = massa (kg).Besarnya momen inersia yang dimiliki oleh benda bergantung kepada beberapa faktor yaitu :
1). Massa benda
2). Bentuk benda
3). Letak sumbu putar
4). Jarak ke sumbu putar.
Empat buah partikel dihubungkan oleh sebuah batang yang massanya diabaikan, ditunjukkan seperti gambar di bawah ini. Tentukan momen inersia sistem partikel bila :
- Diputar terhadap poros A
- Diputar terhadap poros B
Pembahasan :
- Diputar terhadap poros AI = ∑m.R2
⇒ I = 2m (0)2 + 4m (r)2 + m (2r)2 + 2m (3r)2
⇒ I = 0 + 4m r2 + 4m r2 + 18m r2
⇒ I = 26 m r2 - Diputar terhadap poros BI = ∑m.R2
⇒ I = 2m (2r)2 + 4m (r)2 + m (0)2 + 2m (r)2
⇒ I = 8m r2 + 4m r2 + 0 + 2m r2
⇒ I = 14 m r2
Dengan menggunakan rumus pergeseran poros, buktikanlah bahwa momen inersia batang homogen yang diputar pada salah satu ujungnya dapat dihitung dengan rumus I = ⅓ m.l 2.
Pembahasan :
Saat poros bergeser ke salah satu ujung artinya poros digeser sejauh ½l dari pusat, sehingga :
I = 1⁄12 m.l2 + m.(k.l)2
⇒ I = 1⁄12 m.l2 + m.(½.l)2
⇒ I = 1⁄12 m.l2 + ¼ m.l2
⇒ I = (1⁄12 + ¼) m.l2
⇒ I = (1⁄12 + 3⁄12) m.l2
⇒ I = (4⁄12) m.l2
⇒ I = 1⁄3 m.l2 (Terbukti).
Contoh 3 : Momen Inersia Melalui Pusat Batang
A. 1,89 x 10-2 kg m2
B. 1,98 x 10-2 kg m2
C. 2,18 x 10-2 kg m2
D. 2,48 x 10-2 kg m2
E. 2,98 x 10-2 kg m2
Pembahasan :
I = I batang + I lumpur
⇒ I = 1⁄12 m.l2 + mR2
⇒ I = 1⁄12 (0,6).(0,6)2 + 0,02 (0,3)2
⇒ I = 0,018 + 0,0018
⇒ I = 0,0198
⇒ I = 1,98 x 10-2 kg m2
Jawaban : B
Contoh 4 : Momen Inersia Sistem Silinder
Jika sebuah silinder pejal bermassa 2 kg dan berjari-jari 0,1 m diputar melalui sumbu silinder dan segumpal lumpur bermassa 0,2 kg menempel pada jarak 0,05 meter dari pinggir silinder, maka momen inersia sistem adalah ....A. 1,05 x 10-2 kg m2
B. 1,25 x 10-2 kg m2
C. 1,05 x 10-3 kg m2
D. 1,45 x 10-3 kg m2
E. 1,05 x 10-4 kg m2
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.