SOAL DAN PEMBAHASAN SISTEM KATROL BIDANG MIRING

Ketika sistem katrol dipadu dengan bidang miring, maka percepatan yang dialami oleh benda akan bergantung kepada penguraian gaya berat benda dan gaya gesek antara benda dengan bidang miring.

1. Jenis-jenis Gaya
2. Pembahasan Hukum Newton
3. Dinamika Rotasi
4. Pembahasan Sistem Katrol

Sama seperti sistem katrol yang telah dibahas pada artikel sebelumnya, sistem katrol yang dipadu dengan bidang miring juga dikaji berdasarkan ada tidaknya gaya gesek pada bidang miring dan massa katrol.

Berikut akan disajikan empat kemungkinan yang sering terjadi pada sistem katrol dan bidang miring.

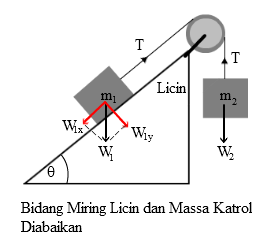
1. Massa Katrol diabaikan dan Bidang Licin
   Ketika massa katrol dibaikan, dan bidang miring licin maka berlaku :
   

   1. Tegangan tali sama (T₁ = T₂ = T)
   2. Tidak ada gaya gesek.

   
   

   

   Pada gambar di atas telah ditunjukkan gaya-gaya yang bekerja pada benda. Pada benda pertama, karena berada pada bidang miring dan gaya berat arahnya ke bawah, maka gaya beratnya harus diuraikan menjadi Wx dan Wy seperti yang terlihat di gambar. Dari gambar jelas terlihat bahwa gaya berat yang berada dalam garis gerak adalah Wx. Jika m₁ < m₂, maka sistem akan bergerak ke arah m₂.
   
   Tinjau benda I :
   ∑F = m.a
   ⇒ T₁ - W_1x = m₁.a
   ⇒ T₁ = m₁.a + W_1x
   ⇒ T = m₁.a + W_1x
   ⇒ T = m₁.a + W₁ sin θ
   
   Tinjau benda II :
   ∑F = m.a
   ⇒ W₂ - T₂ = m₂.a
   ⇒ T₂ = W₂ - m₂.a
   ⇒ T = W₂ - m₂.a
   
   Karena tegangan tali sama besar, maka :
   m₁.a + W₁ sin θ = W₂ - m₂.a
   ⇒ m₁.a + m₂.a = W₂ - W₁ sin θ
   ⇒ (m₁ + m₂) a = W₂ - W₁ sin θ
   ⇒ a = (W₂ - W₁ sin θ)/(m₁ + m₂)
   
   

   a =	W2 − W1 sin θ
   	(m1+ m2)

   
   Dengan :
   a = percepatan sistem (m/s²)
   W₂ = berat benda kedua (N)
   W₁ = berat benda pertama (N)
   m₁ = massa benda pertama (kg)
   m₂ = massa benda kedua (kg)
   θ = sudut kemiringan bidang.
   
   
   
   
2. Massa Katrol diabaikan dan Bidang Kasar
   Ketika massa katrol diabaikan dan bidang miring kasar, maka berlaku :
   

   1. Tegangan tali sama (T₁ = T₂ = T)
   2. Terdapat gaya gesek.

   
   

   

   
   Tinjau benda I :
   ∑F = m.a
   ⇒ T₁ - W_1x - Fg = m₁.a
   ⇒ T₁ = m₁.a + Fg + W_1x
   ⇒ T = m₁.a + Fg + W₁ sin θ
   
   Tinjau benda II :
   ∑F = m.a
   ⇒ W₂ - T₂ = m₂.a
   ⇒ T₂ = W₂ - m₂.a
   ⇒ T = W₂ - m₂.a
   
   Karena tegangan tali sama besar, maka :
   m₁.a + Fg + W₁ sin θ = W₂ - m₂.a
   ⇒ m₁.a + m₂.a = W₂ - Fg - W₁ sin θ
   ⇒ (m₁ + m₂) a = W₂ - Fg - W₁ sin θ
   ⇒ a = (W₂ - Fg - W₁ sin θ)/(m₁ + m₂)
   
   

   a =	W2 − Fg − W1 sin θ
   	(m1+ m2)

   
   Dengan :
   a = percepatan sistem (m/s²)
   W₂ = berat benda kedua (N)
   W₁ = berat benda pertama (N)
   Fg = gaya gesek antara benda 1 dan bidang kasar (N)
   m₁ = massa benda pertama (kg)
   m₂ = massa benda kedua (kg)
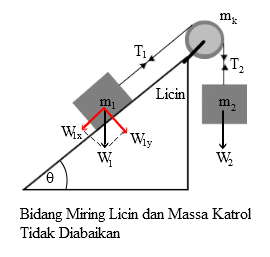
   θ = sudut kemiringan bidang.

   
   
   
   
3. Massa Katrol diketahui dan Bidang Licin
   Ketika massa katrol tidak diabaikan dan bidang miring licin, maka :
   

   1. Tegangan tali tidak sama (T₁ ≠ T₂)
   2. Tidak ada gaya gesek.

   
   

   

   Tinjau benda I :
   ∑F = m.a
   ⇒ T₁ - W_1x = m₁.a
   ⇒ T₁ = m₁.a + W_1x
   ⇒ T₁ = m₁.a + W₁ sin θ
   
   Tinjau benda II :
   ∑F = m.a
   ⇒ W₂ - T₂ = m₂.a
   ⇒ T₂ = W₂ - m₂.a
   
   Tinjau Katrol :
   ∑τ = I.α
   ⇒ T₂.r - T₁.r = k m_k r² . ^a⁄_r
   ⇒ (T₂ - T₁) r = k.m_k.r.a
   ⇒ T₂ - T₁ = k.m_k.a
   
   Substitusi nilai T₁ dan T₂ ke persamaan ketiga, maka :
   T₂ - T₁ = k.m_k.a
   ⇒ W₂ - m₂.a - m₁.a - W₁ sin θ = k.m_k.a
   ⇒ W₂ - W₁ sin θ = k.m_k.a + m₂.a + m₁.a
   ⇒ W₂ - W₁ sin θ = (k.m_k + m₂ + m₁) a
   ⇒ a = (W₂ - W₁ sin θ ) / (k.m_k + m₂ + m₁)
   
   

   a =	W2 − W1 sin θ
   	(k.mk + m2 + m1)

   
   Dengan :
   a = percepatan sistem (m/s²)
   W₂ = berat benda kedua (N)
   W₁ = berat benda pertama (N)
   k = bilangan atau konstanta pada rumus inersia katrol.
   m_k = massa katrol (kg)
   m₁ = massa benda pertama (kg)
   m₂ = massa benda kedua (kg)
   θ = sudut kemiringan bidang.
   
   
   
   
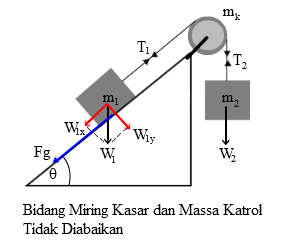
4. Massa Katrol diketahui dan Bidang Kasar
   Jika massa katrol tidak diabaikan dan bidang miring bersifat kasar, maka :
   

   1. Tegangan tali tidak sama (T₁ ≠ T₂)
   2. Terdapat gaya gesek.

   
   

   
   
   Tinjau benda I :
   ∑F = m.a
   ⇒ T₁ - W_1x - Fg = m₁.a
   ⇒ T₁ = m₁.a + Fg + W_1x
   ⇒ T₁ = m₁.a + Fg + W₁ sin θ
   
   Tinjau benda II :
   ∑F = m.a
   ⇒ W₂ - T₂ = m₂.a
   ⇒ T₂ = W₂ - m₂.a
   
   Tinjau Katrol :
   ∑τ = I.α
   ⇒ T₂.r - T₁.r = k m_k r² . ^a⁄_r
   ⇒ (T₂ - T₁) r = k.m_k.r.a
   ⇒ T₂ - T₁ = k.m_k.a
   
   Substitusi nilai T₁ dan T₂ ke persamaan ketiga :
   T₂ - T₁ = k.m_k.a
   ⇒ W₂ - m₂.a - m₁.a - Fg - W₁ sin θ = k.m_k.a
   ⇒ W₂  - Fg - W₁ sin θ = k.m_k.a + m₂.a + m₁.a
   ⇒ W₂ - Fg - W₁ sin θ = (k.m_k + m₂ + m₁) a
   ⇒ a = (W₂ - Fg - W₁ sin θ) / (k.m_k + m₂ + m₁)
   
   

   a =	W2 − Fg − W1 sin θ
   	(k.mk + m1+ m2)

   
   Dengan :
   a = percepatan sistem (m/s²)
   W₂ = berat benda kedua (N)
   W₁ = berat benda pertama (N)
   Fg = gaya gesek antara benda 1 dan bidang kasar (N)
   k = bilangan atau konstanta pada rumus inersia katrol.
   m_k = massa katrol (kg)
   m₁ = massa benda pertama (kg)
   m₂ = massa benda kedua (kg)

   θ = sudut kemiringan bidang.
   
   

Share ke Facebook >>

Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.