HOME

KUMPULAN SOAL DAN PEMBAHASAN TITIK BERAT BENDA

Posted by on 02 April 2015 - 6:10 AM

Titik berat gabungan dari benda-benda teratur yang mempunyai berat, massa, luas, atau volume tertentu dapat dinyatakan dalam koordinat Cartesian (x,y). Rumus menentukan titik koordinat x dan y dari suatu benda telah dibahas pada artikel sebelumnya. Anda dapat membaca artikel cara menentukan titik berat benda untuk mempelajarinya. Pada artikel ini hanya akan dibahas beberapa soal mengenai titik berat benda sebagai berikut.

Contoh Soal
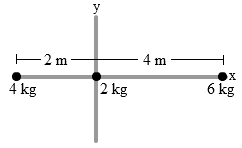
  1. Sistem tiga partikel yang saling dihubungkan dengan bidang ringan tidak bermasa terletak pada satu sistem koordinat seperti pada gambar di bawah ini. Tentukanlah pusat massa sistem.

    titik berat

    Pembahasan :
    x = ma.xa + mb.xb + mc.xc 
          ma + mb + mc
    x = 4(-2) + 2(0) + 6(4) 
          4 + 2 + 6
    x = -8 +  0 + 24
             12
     x = 16⁄12
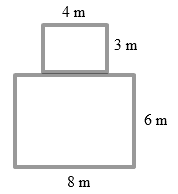
     x = 4⁄3 di kanan massa 2 kg.

  2. Tentukan titik berat benda berupa luasan seperti gambar di bawah ini.

    titik berat

    Pembahasan :
    Ingat bahwa untuk benda persegi, titik beratnya berada di tengah-tengah sebagai berikut :

    titik berat
    Dari gambar di atas jelas terlihat bahwa koordinat titik berat dalam sumbu x adalah x = 4. Dengan begitu kita hanya harus mencari ordinat y saja. Dari soal diketahui :
    ⇒ A1 = 8 x 6 = 48 m2
    ⇒ A2 = 4 x 3 = 12 m2

    Titik ordinat y :
    y = A1.y1 + A2.y2  
       A1 + A2 
    y = 48(3) + 12(7,5) 
         48 + 12
    y = 144 + 90 
          60
      y = 234⁄60
      y = 3,9.

    Jadi, koordinat titik berat benda adalah (4, 3.9).

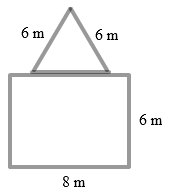
  3. Jika sebuah pelat berbentuk seperti terlihat di bawah ini, tentukanlah titik berat pelat tersebut.

    titik berat

    Pembahasan :
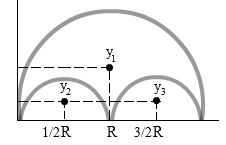
    Agar lebih mudah, kita gambarkan letak titik berat pada masing-masing benda. Kalau kita perhatikan, benda di atas merupakan setengah lingkaran besar yang dipotong oleh dua buah setengah lingkaran yang kecil.

    titik berat

    Kita hitung luasnya, dan ordinatnya masing-masing :
    ⇒ A1 = πR2 
    ⇒ x1 = R ; y1 = 4R⁄3π
    ⇒ A2 = π (½R)2 = ¼ πR2
    ⇒ x2 = ½R ; y2 = 4(½R)⁄3π = 2R⁄3π
    ⇒ A3 = π (½R)2 = ¼ πR2
    ⇒ x3 = 3⁄2 R ; y3 = 4(½R)⁄3π = 2R⁄3π


    Selanjutnya kita hitung koordinat x benda :
    x = A1.x1 − A2.x2 − A3.x3 
          A1 − A2 − A3
    x = πR2 (R) − ¼ πR2 (½R) − ¼ πR2(3⁄2 R) 
               πR2 − ¼ πR2 − ¼ πR2
    x = ½ πR2 (R)
       ½ πR2
     x = R.

    Selanjutnya kita hitung ordinat y benda :
    y = A1.y1 − A2.y2 − A3.y3 
          A1 − A2 − A3
    y = πR2 (4R⁄3π) − ¼πR2 (2R⁄3π) − ¼πR2(2R⁄3π) 
                πR2 − ¼ πR2 − ¼ πR2
    y = 4⁄3 R3 − 1⁄3 R3 
          ½ πR2
     y = 2R⁄π.

    Jadi, koordinat titik beratnya adalah (R ,2R⁄π).

SOAL SERUPA

  • Tentukan koordinat titik berat benda berupa bidang seperti tampak pada gambar ini!
    titik berat
  • titik berat

MENU CONTOH DINAMIKA ROTASI CONTOH SOAL FISIKA
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.