Edutafsi.com - Koordinat Titik Berat. Titik berat suatu benda dapat dinyatakan dalam koordinat Cartesian (x,y). Adakalanya, kita hanya perlu mencari titik ordinat (koordinat y) karena koordinat x (absis) lebih mudah untuk ditentukan. Pada artikel sebelumnya telah dibahas beberapa soal menentukan koordinat titik berat benda berupa massa, dan luasan. Pada kesempatan ini, akan dibahas lebih lanjut beberapa contoh titik berat benda berupa luasan dan volume. Anda dapat membaca cara menentukan titik berat benda untuk mengetahui rumus menentukan titik koordinat benda gabungan, atau anda dapat menyimak beberapa contoh di bawah in.
Contoh 1 : Titik Berat Benda Gabungan
Tentukan koordinat titik berat benda bervolume seperti gambar di bawah ini. Benda terdiri dari silinder pejal dan setengah bola pejal.
Tentukan koordinat titik berat benda bervolume seperti gambar di bawah ini. Benda terdiri dari silinder pejal dan setengah bola pejal.
Dari gambar langsung dapat kita tentukan bahwa titik koordinat x (absis) yaitu x = ½r. Akan tetapi agar lebih paham, akan kita bahas bagaimana perhitungannya. Pada gambar diameter silinder dinyatakan dengan r maka kita misalkan saja jari-jarinya R, dengan R = ½r. Tinggi tabung adalah 2r atau sama dengan 4R karena r = 2R.
Dari soal kita peroleh :
⇒ V1 = ½ volume bola = ½. 4⁄3 πR3 = ⅔ πR3
⇒ x1 = ½ r = R
⇒ y1 = 3⁄8 R + 2r = 3⁄8 R + 4R = 35⁄8 R
⇒ V2 = volume silinder = πR2 (t) = πR2 (4R) = 4 πR3
⇒ x2 = ½ r = R
⇒ y2 = ½ t = ½ (4R) = 2R
Menentukan titik x :
| x = | V1.x1 + V2.x2 |
| V1 + V2 |
| x = | ⅔ πR3 (R) + 4 πR3 (R) |
| ⅔ πR3 + 4 πR3 |
| x = | (⅔ πR3 + 4 πR3) R |
| ⅔ πR3 + 4 πR3 |
Catatan : jika x1 = x2, maka x = x1 = x2.
Menentukan ordinat y :
| ⇒ y = | V1.y1 + V2.y2 |
| V1 + V2 |
| ⇒ y = | ⅔ πR3 (35⁄8 R) + 4 πR3 (2R) |
| ⅔ πR3 + 4 πR3 |
| ⇒ y = | (2,9 πR3 + 8 πR3) R |
| 4,66 πR3 |
⇒ y = 1,17 r.
Jadi, koordinat titik beratnya : (R, 2.34R) atau (½ r, 1.17 r).
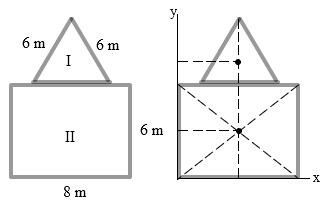
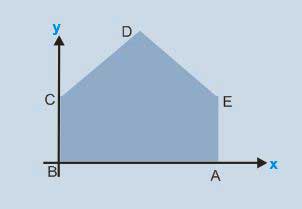
Tentukan koordinat titik berat benda berupa bidang seperti tampak pada gambar.
Pembahasan :
Jika kita perhatikan gambar, maka koordinat x dapat kita jawab tanpa menggunakan rumus, yaitu x = 4 m. Jadi kita tinggal menghitung ordinat y saja sebagai berikut :
Dari soal kita peroleh :
⇒ A1 = luas segitiga = ½.(6) (3√3) = 15,6 m2
⇒ y1 = ⅓t + 6 = ⅓ (3√3) + 6 = 7,7 m
⇒ A2 = luas persegi = 8 (6) = 48 m2
⇒ y2 = ½ t = ½ (6) = 3 m.
Tentukan ordinat y :
⇒ y = 4,15 m.
Jadi, koordinat titik berat benda : (4, 4.15).
⇒ A1 = luas segitiga = ½.(6) (3√3) = 15,6 m2
⇒ y1 = ⅓t + 6 = ⅓ (3√3) + 6 = 7,7 m
⇒ A2 = luas persegi = 8 (6) = 48 m2
⇒ y2 = ½ t = ½ (6) = 3 m.
Tentukan ordinat y :
| ⇒ y = | A1.y1 + A2.y2 |
| A1 + A2 |
| ⇒ y = | 15,6 (7,7) + 48 (3) |
| 15,6 + 48 |
| ⇒ y = | 120,12 + 144 |
| 63,6 |
| ⇒ y = | 264,12 |
| 63,6 |
Jadi, koordinat titik berat benda : (4, 4.15).
SOAL SERUPA
- UN Matematika
Karton homogen ABCDE dengan ukuran AB = EC = 8 cm, AE = 4 cm, ED = CD = 5 cm. Jarak titik berat karton dihitung dari garis AB adalah .....
A. 1,5 m
B. 2,0 m
C. 2,8 m
D. 4,5 m
E. 6,0 m
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.