CONTOH SOAL DAN JAWABAN DIMENSI DAN PENJUMLAHAN VEKTOR

Pada umumnya, besaran turunan merupakan besaran vekor yaitu besaran yang memiliki nilai dan arah misalnya kecepatan, gaya, perpindahan dan sebagainya. Besaran yang hanya memiliki nilai saja disebut besaran skalar misalnya massa, waktu, jarak, kelajuan, dan sebagainya.

Jika berbicara mengenai besaran vektor, maka yang menjadi fokus kita adalah nilai dan arah. Analisis arah sangat menentukan hasil yang diperoleh. Cara yang paling umum digunakan untuk menentukan resultan dua vektor adalah dengan aturan cosinus.

Untuk vektor-vektor yang segaris, resultan vektornya dapat dihitung dengan cara menjumlahkan atau mengurangkan vektor-vektor tersebut secara aljabar biasa. Di bawah ini dibahas beberapa contoh.

Contoh Soal :

1. Persaman gas ideal memenuhi persamaan PV/T = C, dengan C adalah konstanta. Berdasarkan rumus tersebut, dimensi dari konstanta C adalah .....

   A. [M][L]-2[T]-3[θ]-1	D. [M][L]-2[T]-3[θ]-2
   B. [M][L]2[T]-3[θ]-1	E. [M][L]-2[T]-2[θ]-1
   C. [M][L]2[T]-2[θ]-1

   
   Pembahasan :
   Berikut tabel besaran pokok, satuan, dan dimensinya.
   

   Besaran	Satuan	Dimensi
   Panjang	meter (m)	L
   Massa	kilogram (kg)	M
   Waktu	sekon (s)	T
   Suhu	Kelvin (K)	θ

   
   Yang perlu kita ingat adalah dimensi untuk besaran-besaran pokok seperti yang terlihat pada tabel. Selanjutnya kita nyatakan besaran turunan yang sesuai.
   ⇒ C = PV/T
   ⇒ C = {(F/A).V}/T
   ⇒ C = FV/AT
   ⇒ C = (m.a.V)/AT
   ⇒ C = (kg.m/s².m³)/(m².K)
   ⇒ C = kg.m².s^-2.K^-1
   ⇒ C = (massa).(panjang)².(waktu)^-2.(suhu)^-1
   ⇒ C = [M][L]²[T]^-2[θ]^-1
   

   Jawaban : C

   
   
2. Perhatikan tabel di bawah ini.

   No	Dimensi	Besaran	Satuan
   1	ML2T-2	Usaha	Joule
   2	M-1L3T-2	Konstanta Gravitasi	m/s2
   3	ML2T-2	Torsi	N.m

   
   Pasangan dimensi, besaran, dan satuan yang sesuai adalah ....
   

   A. 1 dan 2	D. 1, 2, dan 3
   B. 1 dan 3	E. Hanya 2
   C. 2 dan 3

   
   Pembahasan :
   Karena lebih mudah menyusun dimensi berdasarkan rumus daripada menyusun rumus berdasarkan dimensi, maka kita dapat menggunakan rumus untuk mengetahui pasangan yang sesuai :
   

   1. Usaha
      ⇒ W= F.s 
      ⇒ W= m.a.s
      ⇒ W= m.(v/t).s
      ⇒ W= m.(s/t²).s
      ⇒ W = kg.m²/s²
      ⇒ W = (massa).(panjang)²/(waktu)²
      ⇒ W = (massa).(panjang)².(waktu)^-2
      ⇒ W = [M][L]²[T]^-2
      ∴ Dimensi dan satuan sesuai.
      
      
   2. Konstanta Gravitasi
      ⇒ G = (F.r²)/(m₁.m₂)
      ⇒ G = (m.a.r²)/(m₁.m₂)
      ⇒ G = (kg.m/s².m²)/(kg²)
      ⇒ G = m³/s²kg
      ⇒ G = m³s^-2kg^-1
      ⇒ G = (panjang)³.(waktu)^-2.(massa)^-1
      ⇒ G = [M]^-1.[L]³.[T]^-2
      ∴ Dimensi sesuai, satuan tidak.
      
      
   3. Torsi
      τ = F.d
      ⇒ τ = m.a.d
      ⇒ τ = (m).(v/t).(d)
      ⇒ τ = (m).(s/t²).(d)
      ⇒ τ = kg.m²/s²
      ⇒ τ = (massa).(panjang²/waktu²)
      ⇒ τ = [M].[L]².[T]^-2
      ∴ Dimensi dan satuan sesuai.

   Jawaban : B
   
   
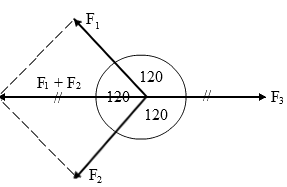
3. Jika tiga buah vektor yang sama besar berada pada satu titik tangkap dan saling membentuk sudut 120o,  maka resultan gayanya adalah .....

   A. Sama besar dengan tiap vektor	D. Setengah besar vektor
   B. Dua kali besar vektor	E. Tiga kali besar vektor
   C. Nol

   
   Pembahasan :
   Jika kita gambar sketsanya kurang lebih akan seperti di bawah ini.
   

   

   Dari gambar di atas jelas terlihat bahwa resultan F1 dan F2 sama besar dengan vektor F3 akan tetapi berlawanan arah (F1 + F2 = -F3) sehingga resultan totalnya adalah :
   ⇒ R = F1 + F2 + F3
   ⇒ R = -F3 + F3
   ⇒ R = 0
   
   Jawaban di atas juga dapat dibuktikan dengan aturan cosinus sebagai berikut :
   ⇒ F1 + F2 = √F₁² + F₂² + 2F₁F₂ cos θ
   ⇒ F1 + F2 = √F² + F² + 2F.F cos 120^o
   ⇒ F1 + F2 = √2F² + 2F² (-½)
   ⇒ F1 + F2 = √2F² - F² 
   ⇒ F1 + F2 = √F² 
   ⇒ F1 + F2 = F
   ⇒ F1 + F2 = F
   Tanda negatif karena F1 + F2 pasti berlawanan arah dengan F3 namun sama besar. Dengan demikian resultannya adalah :
   ⇒ R = F1 + F2 + F3

   ⇒ R = -F3 + F3
   ⇒ R = 0
   Jawaban : C
   
   
4. Dua buah gaya sama besar sebesar F berada pada satu titik tangkap. Jika resultannya kedua gaya sama dengan √3 kali besar gaya tersebut, maka besar sudut apit kedua gaya adalah .....

   A. 120o	D. 37o
   B. 90o	E. 30o
   C. 60o

   
   Pembahasan :
   Dik : F₁ = F₂ = F, dan R = F.
   
   Resultan dua buah gaya yang membentuk sudut apit dapat dihitung dengan menggunakan aturan kosinus sebagai berikut :
   ⇒ R =  √F₁² + F₂² + 2F₁F₂ cos θ
   ⇒ √3F =  √F² + F² + 2F.F cos θ
   ⇒ √3F =  √2F² + 2F² cos θ
   ⇒ (√3F)² = 2F² + 2F² cos θ
   ⇒ 3F² = 2F² + 2F² cos θ
   ⇒ F² = 2F² cos θ
   ⇒ ½ = cos θ
   ⇒ θ = 60^o
   

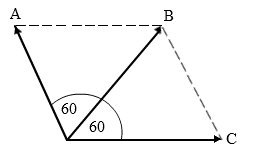
   Jawaban : C
   
   
5. Tiga buah vektor A, B, dan C yang setitik tangkap masing-masing besarnya 20 N. Vektor B berada di antara A dan C. Jika sudut antara A dan B sama dengan sudut antara B dan C yaitu 60^o, maka resultan ketiga vektor tersebut adalah ....

   A. 10	D. 40
   B. 20	E. 50
   C. 30

   
   Pembahasan :
   Diketahui : A = B = C = 20 N. 
   

   

   
   

   Dari gambar di atas jelas terlihat bahwa A + C = B. Dengan demikian resultannya adalah :
   ⇒ R = A + B + C
   ⇒ R = B + B  
   ⇒ R = 2B
   ⇒ R = 2(20)
   ⇒ R = 40 N.
   
   Jawaban di atas juga dapat dibuktikan dengan aturan cosinus. Sudut yang dibentuk oleh A dan C adalah 120^o, sehingga :
   ⇒ A + C = √A² + C² + 2A.C cos θ
   ⇒ A + C = √A² + A² + 2A.A cos 120^o
   ⇒ A + C = √2A² + 2A² (-½)
   ⇒ A + C = A
   Karena A = B = C = 20 N, maka :
   ⇒ R = A + B + C
   ⇒ R = A + C + B
   ⇒ R = A + B
   ⇒ R = 20 + 20
   ⇒ R = 40 N.
   

   Jawaban : D

Share ke Facebook >>

Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.