Edutafsi.com - (Contoh 7 : Menentukan Titik Minimum Fungsi Ojektif). Sebuah perusahaan properti memproduksi dua macam lemari pakaian yaitu tipe lux dan tipe sport dengan menggunakan 2 bahan dasar yang sama yaitu kayu jati dan cat pernis. Untuk memproduksi 1 unit tipe lux dibutuhkan 10 batang kayu jati dan 3 kaleng cat pernis, sedangkan untuk memproduksi 1 unit tipe sport dibutuhkan 6 batang kayu jati dan 1 kaleng cat pernis. Biaya produksi tipe lux dan tipe sport masing-masing adalah Rp 40.000 dan Rp 28.000 per unit. Untuk satu periode produksi, perusahaan menggunakan paling sedikit 120 batang kayu jati dan 24 kaleng cat pernis. Bila perusahaan harus memproduksi lemari tipe lux paling sedikit 2 buah dan tipe sport paling sedikit 4 buah, tentukan banyak lemari tipe lux dan tipe sport yang harus diproduksi agar biaya produksinya minimum.
Pembahasan:
Karena yang ditanya adalah biaya produksi minimum, maka ongkos produksi masing-masing tipe lemari merupakan fungsi tujuannya. Oleh karena itu, kita dapat melakukan pemisalan variabel sebagai berikut:
1). Banyak lemari tipe lux = x
2). Banyak lemari tipe sport = y
Jika dinyatakan dalam variabel x dan y, maka fungsi tujuannya adalah:
F(x, y) = 40.000x + 28.000y
Arti dari fungsi tujuan di atas adalah berapa nilai x (banyak lemari tipe lux) dan nilai y (banyak lemari tipe sport) agar nilai F minimum. Dengan kata lain, berapa jumlah lemari tipe lux dan tipe sport yang harus diperoduksi agar modal produksi minimum.
Selanjutnya, model matematika untuk kendala yang diberikan adalah seperti di bawah ini. Perhatikan bahwa tanda pertidaksamaan yang digunakan untuk soal penentuan nilai minimum adalah lebih besar dari sama dengan (≥) seperti di bawah ini :
1). Jumlah lemari tipe lux paling sedikit 2 → x ≥ 2
2). Jumlah lemari tipe sport paling sedikit 4 → y ≥ 4
3). Kayu jati paling sedikit 120 batang → 10x + 6y ≥ 120
4). Cat pernis paling sedikit 24 kaleng → 3x + y ≥ 24
Titik potong masing-masing kendala terhadap sumbu x dan sumbu y adalah sebagai berikut :
Untuk 10x + 6y = 120
1). misal x = 0, maka y = 20 → titik potong (0,20)
2). misal y = 0, maka x = 12 → titik potong (12,0)
Untuk 3x + y = 24
1). misal x = 0, maka y = 24 → titik potong (0,24)
2). misal y = 0, maka x = 8 → titik potong (8,0)
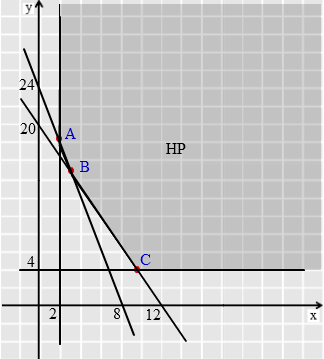
Setelah itu kita gambarkan grafik sesuai dengan titik-titik yang telah kita peroleh dan tentukan daerah himpunan penyelesaiannya. Karena lebih besar sama dengan (≥), maka daerah himpunan penyelesaiannya adalah daerah di atas/kanan garis.
Dari garfik di atas jelas terlihat bahwa terdapat tiga titik pojok yang akan diuji untuk dilihat titik manakah yang menghasilkan nilai minimum.
Titik C merupakan perpotongan antara garis y = 4 dan 10x + 6y = 120. Dengan mensubstitusi nilai y = 4 pada persamaan 10x + 6y = 120, maka diperoleh :
⇒ 10x + 6(4) = 120
⇒ 10x = 96
⇒ x = 9,6
⇒ x = 9 → digenapkan 9 karena tidak mungkin 0,6 buah.
Jadi titik C(9,4)
Titik B merupakan perpotongan antara garis 10x + 6y = 120 dan garis 3x + y = 24. Dengan metode substitusi diperoleh :
⇒ 3x + y = 24
⇒ y = 24 - 3x
Substitusi ke persamaan 10x + 6y = 120, diperoleh :
⇒ 10x + 6(24 - 3x) = 120
⇒ 10x + 144 - 18x = 120
⇒ -8x = -24
⇒ x = 3
Sunstitusi x = 3 ke persamaan y = 24 - 3x, diperoleh :
⇒ y = 24 - 3(3)
⇒ y = 15
Jadi, titik B(3,15)
Titik A merupakan perpotongan antara garis 3x + y = 24 dengan x = 2. Dengan mensubstitusikan nilai x pada persamaan 3x + y = 24, maka diperoleh :
⇒ 3(2) + y = 24
⇒ y = 24 - 6
⇒ y = 18
Jadi, titik A(2,18)
Langkah terakhir, substitusi masing-masing titik ke fungsi tujuan F(x, y) = 40.000x + 28.000y sebagai berikut:
1). A(2, 18) → F(x,y) = 40.000(2) + 28.000(18) = 584.000
2). B(3, 15) → F(x,y) = 40.000(3) + 28.000(15) = 540.000
3). C(9, 4) → F(x,y) = 40.000(9) + 28.000(4) = 482.000
Dari perhitungan di atas dapat dilihat bahwa titik yang menghasilkan nilai minimum adalah titik C(9, 4). Jadi agar biaya produksi minimum, perusahaan sebaiknya memproduksi 9 buah lemari tipe lux dan 4 buah lemari tipe sport dengan biaya produksi Rp 482.000,00
Contoh 8 : Menentukan Nilai Minimum Fungsi Tujuan
Seorang pedagang furnitur ingin mengirim barang dagangannya yang terdiri atas 1.200 kursi dan 400 meja. Untuk keperluan tersebut, ia akan menyewa truk dan colt. Truk dapat memuat 30 kursi lipat dan 20 meja lipat, sedangkan colt dapat memuat 40 kursi lipat dan 10 meja lipat. Ongkos sewa sebuah truk Rp 200.000,00 sedangkan ongkos sewa sebuah colt Rp 160.000,00. Tentukan jumlah truk dan colt yang harus disewa agar ongkos pengiriman minimum.
Baca juga : Pembahasan Nilai Minimum Fungsi Tujuan >>
Contoh 9 : Menentukan Nilai Minimum Fungsi Objektif
Seorang petani memiliki tanah tidak kurang dari 10 hektar. Ia merencanakan akan menanami padi seluas 2 hektar sampai dengan 6 hektar dan menanam jagung seluas 4 hektar sampai dengan 6 hektar. Untuk menanam padi perhektarnya diperlukan biaya Rp 400.000,00 sedangkan untuk menanam jagung per hektarnya diperlukan biaya Rp 200.000,00. Agar biaya tanam minimum, tentukan berapa banyak masing-masing padi dan jagung yang harus ditanam.
Baca juga : Pembahasan Nilai Minimum Fungsi Objektif >>
Pembahasan:
Karena yang ditanya adalah biaya produksi minimum, maka ongkos produksi masing-masing tipe lemari merupakan fungsi tujuannya. Oleh karena itu, kita dapat melakukan pemisalan variabel sebagai berikut:
1). Banyak lemari tipe lux = x
2). Banyak lemari tipe sport = y
Jika dinyatakan dalam variabel x dan y, maka fungsi tujuannya adalah:
F(x, y) = 40.000x + 28.000y
Arti dari fungsi tujuan di atas adalah berapa nilai x (banyak lemari tipe lux) dan nilai y (banyak lemari tipe sport) agar nilai F minimum. Dengan kata lain, berapa jumlah lemari tipe lux dan tipe sport yang harus diperoduksi agar modal produksi minimum.
Selanjutnya, model matematika untuk kendala yang diberikan adalah seperti di bawah ini. Perhatikan bahwa tanda pertidaksamaan yang digunakan untuk soal penentuan nilai minimum adalah lebih besar dari sama dengan (≥) seperti di bawah ini :
1). Jumlah lemari tipe lux paling sedikit 2 → x ≥ 2
2). Jumlah lemari tipe sport paling sedikit 4 → y ≥ 4
3). Kayu jati paling sedikit 120 batang → 10x + 6y ≥ 120
4). Cat pernis paling sedikit 24 kaleng → 3x + y ≥ 24
Titik potong masing-masing kendala terhadap sumbu x dan sumbu y adalah sebagai berikut :
Untuk 10x + 6y = 120
1). misal x = 0, maka y = 20 → titik potong (0,20)
2). misal y = 0, maka x = 12 → titik potong (12,0)
Untuk 3x + y = 24
1). misal x = 0, maka y = 24 → titik potong (0,24)
2). misal y = 0, maka x = 8 → titik potong (8,0)
Setelah itu kita gambarkan grafik sesuai dengan titik-titik yang telah kita peroleh dan tentukan daerah himpunan penyelesaiannya. Karena lebih besar sama dengan (≥), maka daerah himpunan penyelesaiannya adalah daerah di atas/kanan garis.
Dari garfik di atas jelas terlihat bahwa terdapat tiga titik pojok yang akan diuji untuk dilihat titik manakah yang menghasilkan nilai minimum.
Titik C merupakan perpotongan antara garis y = 4 dan 10x + 6y = 120. Dengan mensubstitusi nilai y = 4 pada persamaan 10x + 6y = 120, maka diperoleh :
⇒ 10x + 6(4) = 120
⇒ 10x = 96
⇒ x = 9,6
⇒ x = 9 → digenapkan 9 karena tidak mungkin 0,6 buah.
Jadi titik C(9,4)
Titik B merupakan perpotongan antara garis 10x + 6y = 120 dan garis 3x + y = 24. Dengan metode substitusi diperoleh :
⇒ 3x + y = 24
⇒ y = 24 - 3x
Substitusi ke persamaan 10x + 6y = 120, diperoleh :
⇒ 10x + 6(24 - 3x) = 120
⇒ 10x + 144 - 18x = 120
⇒ -8x = -24
⇒ x = 3
Sunstitusi x = 3 ke persamaan y = 24 - 3x, diperoleh :
⇒ y = 24 - 3(3)
⇒ y = 15
Jadi, titik B(3,15)
Titik A merupakan perpotongan antara garis 3x + y = 24 dengan x = 2. Dengan mensubstitusikan nilai x pada persamaan 3x + y = 24, maka diperoleh :
⇒ 3(2) + y = 24
⇒ y = 24 - 6
⇒ y = 18
Jadi, titik A(2,18)
Langkah terakhir, substitusi masing-masing titik ke fungsi tujuan F(x, y) = 40.000x + 28.000y sebagai berikut:
1). A(2, 18) → F(x,y) = 40.000(2) + 28.000(18) = 584.000
2). B(3, 15) → F(x,y) = 40.000(3) + 28.000(15) = 540.000
3). C(9, 4) → F(x,y) = 40.000(9) + 28.000(4) = 482.000
Dari perhitungan di atas dapat dilihat bahwa titik yang menghasilkan nilai minimum adalah titik C(9, 4). Jadi agar biaya produksi minimum, perusahaan sebaiknya memproduksi 9 buah lemari tipe lux dan 4 buah lemari tipe sport dengan biaya produksi Rp 482.000,00
Contoh 8 : Menentukan Nilai Minimum Fungsi Tujuan
Baca juga : Pembahasan Nilai Minimum Fungsi Tujuan >>
Contoh 9 : Menentukan Nilai Minimum Fungsi Objektif
Seorang petani memiliki tanah tidak kurang dari 10 hektar. Ia merencanakan akan menanami padi seluas 2 hektar sampai dengan 6 hektar dan menanam jagung seluas 4 hektar sampai dengan 6 hektar. Untuk menanam padi perhektarnya diperlukan biaya Rp 400.000,00 sedangkan untuk menanam jagung per hektarnya diperlukan biaya Rp 200.000,00. Agar biaya tanam minimum, tentukan berapa banyak masing-masing padi dan jagung yang harus ditanam.
Baca juga : Pembahasan Nilai Minimum Fungsi Objektif >>
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.