Edutafsi.com - Momen Inersia. Momen inersia adalah besaran fisika yang digunakan untuk menyatakan kecenderungan benda mempertahankan posisinya dalam gerak rotasi. Dengan kata lain, momen inersia bisa dikatakan sebagai besaran massa untuk gerak rotasi. Secara umum, besar momen inersia suatu benda merupakan hasil kali dari massa dan kuadrat jarak titik poros. Meski begitu ada beberapa poin penting yang harus diperhatikan dalam penentuan momen inersia termasuk letak sumbu putarnya.
Untuk beberapa benda khusus seperti partikel titik, batang homogen, silinder, dan bola pejal, momen inersia dapat ditentukan dengan rumus tertentu. Pada kesempatan ini Edutafsi akan membahas rumus momen inersia dari beberapa benda khusus.
Keterangan :
I = momen inersia (kg m2)
Untuk beberapa benda khusus seperti partikel titik, batang homogen, silinder, dan bola pejal, momen inersia dapat ditentukan dengan rumus tertentu. Pada kesempatan ini Edutafsi akan membahas rumus momen inersia dari beberapa benda khusus.
A. Benda Berupa Titik
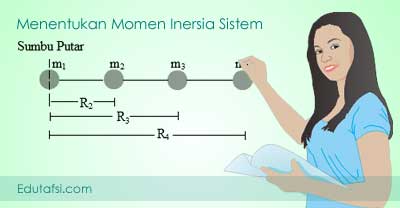
Untuk massa berupa titik atau sistem massa yang terdiri dari beberapa
titik dan terhubung oleh tali atau batang yang massanya diabaikan seperti yang terlihat pada gambar di bawah ini,
berlaku :
| I = ∑m.R2 = m1.R12 + m2.R22 + m3.R32 |
Keterangan :
I = momen inersia (kg m2)
R = jarak ke titik poros (m)
m = massa (kg).B. Batang Homogen
Batang homogen adalah batang yang massanya tersebar merata sehingga pusat massanya berada di tengah. Untuk batang homogen, maka akan jelas terlihat bahwa terdapat pengaruh letak sumbu putar terhadap momen inersia.
#1 Poros di Pusat
#2 Poros di salah satu ujung
#3 Poros bergeser
Panjang pergeseran yang dimaksud di atas adalah seberapa jauh sumbu putarnya digeser misalnya dari pusat digeser ke kanan sejauh ¼l .
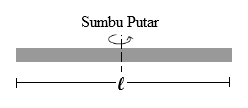
#1 Poros di Pusat
Jika sumbu putar berada di titik pusat massanya maka berlaku :
Keterangan :
I = momen inersia (kg m2)
| I = 1⁄12 m.l2 |
Keterangan :
I = momen inersia (kg m2)
l = panjang batang (m)
m = massa (kg).
Jika sumbu putar berada pada salah satu ujung batang, maka :
Keterangan :
I = momen inersia (kg m2)
| I = ⅓ m.l 2 |
Keterangan :
I = momen inersia (kg m2)
l = panjang batang (m)
m = massa (kg)
Jika sumbu putar atau porosnya berada di sembarang tempat (tidak di ujung atau di pusat), maka momen inersia dapat dihitung dengan rumus berikut :
Keterangan :
I = momen inersia (kg m2)
| I = 1⁄12 m.l2 + m.(k.l)2 |
Keterangan :
I = momen inersia (kg m2)
l = panjang batang (m)
k.l = panjang pergeseran (m)
m = massa (kg)k.l = panjang pergeseran (m)
Panjang pergeseran yang dimaksud di atas adalah seberapa jauh sumbu putarnya digeser misalnya dari pusat digeser ke kanan sejauh ¼l .
C. Benda Berbentuk Silinder
#1 Silinder Pejal
#2 Silinder Tipis Berongga
#3 Silinder Berongga Tidak Tipis
Untuk benda yang berbentuk silinder pejal seperti katrol atau roda tertentu, maka momen inersianya dapat dihitung dengan rumus berikut :
Keterangan :
I = momen inersia (kg m2)
| I = ½ m.R2 |
Keterangan :
I = momen inersia (kg m2)
R = jari-jari silinder (m)
m = massa (kg).
Untuk silinder tipis berongga seperti cincin tipis maka momen inersianya dapat dihitung dengan rumus berikut:
Keterangan :
I = momen inersia (kg m2)
| I = m.R2 |
Keterangan :
I = momen inersia (kg m2)
R = jari-jari silinder (m)
m = massa (kg)
Silinder berongga tidak tipis merupakan silinder yang memiliki jari-jari dalam dan jari-jari luar. Untuk benda seperti ini maka berlaku :
Keterangan :
I = momen inersia (kg m2)
R1 = jari-jari dalam silinder (m)
R2 = jari-jari luar silinder (m)
m = massa (kg).
| I = ½ m (R12 + R22) |
Keterangan :
I = momen inersia (kg m2)
R1 = jari-jari dalam silinder (m)
R2 = jari-jari luar silinder (m)
m = massa (kg).
D. Benda Berbentuk Bola
#1 Bola Pejal
#2 Bola Berongga
Jika benda berbentuk bola peal, maka momen inersianya dapat dihitung dengan rumus berikut :
Keterangan :
I = momen inersia (kg m2)
| I = ⅖ m.R2 |
Keterangan :
I = momen inersia (kg m2)
R = jari-jari bola (m)
m = massa (kg)
Untuk bola berongga berlaku :
Keterangan :
I = momen inersia (kg m2)
Demikianlah pembahasan singkat mengenai rumus momen inersia beberapa benda khusus. Jika artikel yag anda baca bermanfaat, silahkan bagikan kepada teman anda melalui tombol share di bawah ini.
| I = ⅔ m.R2 |
Keterangan :
I = momen inersia (kg m2)
R = jari-jari bola (m)
m = massa (kg).Demikianlah pembahasan singkat mengenai rumus momen inersia beberapa benda khusus. Jika artikel yag anda baca bermanfaat, silahkan bagikan kepada teman anda melalui tombol share di bawah ini.
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.