Edutafsi.com - Kedudukan Titik Dalam Ruang. Istilah titik, garis, dan bidang merupakan tiga istilah dasar yang akan dibahas saat mempelajari tentang geometri. Jika berbicara mengenai geometri dalam suatu bangun ruang, maka titik, garis, dan bidang merupakan tiga hal yang saling berhubungan. Hubungan ketiga istilah tersebut dapat dinyatakan berdasarkan kedudukan relatif antara satu dengan lainnya. Lalu, bagaimana kedudukan sebuah titik terhadap garis dan bidang di dalam suatu ruang? Pada kesempatan ini, edutafsi akan memaparkan pengertian titik, garis, dan bidang serta menyatakan kedudukan titik terhadap garis dan bidang.
#1 Titik
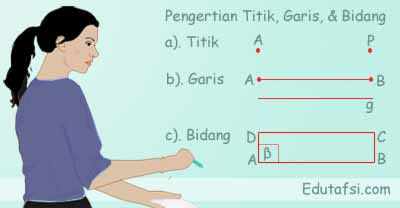
Titik merupakan istilah yang sudah tidak asing lagi bagi kita. Ditulis dengan noktah "." titik termasuk karakter yang sering kita gunakan dalam tulisan. Dalam kegiatan menulis, tanda titik umumnya digunakan untuk mengakhiri sebuah kalimat atau menyertai singkatan tertentu yang harus dibubuhi tanda titik. Lalu, apakah pengertian tersebut sama dengan titik dalam topik geometri?
Dalam kajian geometri, titik merupakan sebuah istilah yang digambarkan dengan menggunakan tanda noktah (.) yang kemudian dibubuhi nama titik tersebut. Titik memiliki kedudukan relatif terhadap garis dan bidang namun tidak terbatas terhadap ukuran. Artinya, benda langit seperti bintang yang jauh di angkas juga dapat dipandang sebagai kumpulan titik meskipun ukuran bintang tersebut sebenarnya lebih besar dari bumi.
Nama sebuah titik umumnya ditulis menggunakan huruf kapital (misalnya titik A, titik P, dan sebagainya) dan diletakkan di dekat titik tersebut. Nama tersebut berfungsi sebagai penjelas titik atau sebagai pengenal titik. Pemberian nama dimaksudkan agar kedudukan sebuah titik dapat dinyatakan dengan jelas terhadap garis atau bidang.
#2 Garis
Dari dua buah titik yang terpisah pada jarak tertentu dapat ditarik sebuah garis lurus yang biasanya akan diberi nama sesuai dengan nama titik yang dihubungkan. Misal titik yang dihubungkan adalah titik A dan B, maka garis yang terbentuk adalah garis AB. Panjang garis yang terbentuk sama dengan jarak terdekat antara titik A dan B.
Sebuah garis lurus dapat diperpanjang sesuai kebutuhan namun umumnya sebuah garis digambarkan sebagian saja sebagai wakil dari suatu garis. Sebuah garis memiliki ukuran panjang yang dinyatakan dengan satuan panjang (meter, cm, dan sebagainya) namun tidak memiliki ukuran lebar. Artinya, ketebalan sebuah garis umumnya diabaikan karena relatif tipis.
Selain dinyatakan berdasarkan titik-titik di kedua ujungnya yang dihubungkan, nama dari sebuah garis juga dapat dinyatakan dengan menggunakan nama yang mewakili garis tersebut. Untuk metode ini biasanya digunakan huruf kecil (misal garis k, garis l, garis g, dan sebagainya). Pada contoh gambar di atas, terdapat garis g atau disebut juga segmen garis AB.
#3 Bidang
Dari tiga atau lebih titik dapat dihasilkan sebuah bidang. Ketika tiga titik yang terpisah pada jarak tertentu dihubungkan dengan garis maka dapat dihasilkan sebuah bidang berbentuk segitiga. Tentu sja bentuk bidang yang dihasilkan bergantung pada posisi titik terhadap titik lainnya. Begitu pula pada bidang yang berbentuk persegi, bidang tersebut bisa saja diperoleh dari empat titik yang dihubungkan dengan garis lurus.
Bidang yang terbentuk dari hubungan tiga atau lebih titik seperti yang dijelaskan di atas umumnya diberi nama sesuai dengan nama titik-titik yang dihubungkan. Misalnya sebuah bidang berbentuk segitiga dihasilkan dari tiga buah titik yaitu titik A, B, dan C, maka bidang tersebut dapat dinamai sebagai bidang ABC.
Jika diperhatikan, sebuah bidang tidak hanya terbentuk dari adanya beberapa titik, tapi juga karena adanya beberapa garis yang saling dihubungkan. Dengan demikian, bidang juga dapat diartikan sebagai himpunan garis-garis yang anggotanya lebih dari dua garis. Misalnya bidang berbentuk segitiga terdiri dari tiga buah garis yang saling bertemu di kedua ujungnya.
Selain diberi nama berdasarkan titik-titik di sudut bidang tersebut, sebuah bidang biasanya juga dapat dinamai dengan menggunakan huruf yunani (α, β, γ) atau huruf kapital (H, U, V, W) yang diletakkan di salah satu sudut bidang tersebut.
#1 Titik Terletak Pada Garis
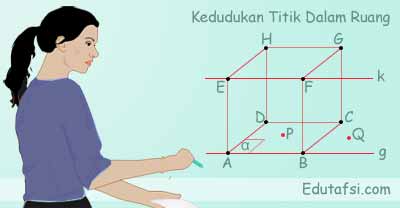
Sebuah titik dikatakan terletak pada garis jika titik tersebut dilalui oleh garis atau titik tersebut bersentuhan tepat dengan segmen garis. Misalnya titik A dilalui oleh garis g, maka titik A dikatakan terletak pada garis. Pada contoh gambar di bawah, titik A dan titik B disebut terletak pada segmen garis g.
#2 Titik di Luar Garis
Jika sebuah titik tidak dilalui oleh sebuah garis, maka titik tersebut dikatakan berada di luar garis. Sebagai contoh, pada gambar kubus di bawah, titik A dan titik B dikatakan terletak di luar garis k, karena tidak dilalui oleh garis tersebut.
#1 Titik Terletak Pada Bidang
Sebuah titik dikatakan terletak pada bidang jika titik tersebut dapat dilalui oleh bidang. Sebagai contoh perhatikan gambar kubus di atas. Pada gambar tersebut, titik P dikatakan terletak pada bidang α karena titik tersebut dilalui oleh bidang (titik P menempel tepat di bidang α).
#2 Titik di Luar Bidang
Jika sebuah titik tidak dapat dilalui oleh bidang, maka titik tersebut dikatakan berada di luar bidang. Sebagai contoh, pada gambar kubus di atas, titik Q disebut berada di luar bidang α karena bidang α tidak dapat melalui titik tersebut.
Demikianlah pembahasan singkat mengenai cara menyatakan kedudukan sebuah titik terhadap garis dan bidang di dalam suatu ruang tiga dimensi. Jika bahan belajar ini bermanfaat, bantu kami membagikannya kepada teman-teman anda melalui tombol share yang tersedia di bawah ini. Terimakasih.
A. Pengertian Titik, Garis, dan Bidang
Sebuah ruang tiga dimensi terdiri dari beberapa unsur dasar, yaitu titik, garis, dan bidang. Suatu bangun ruang terbentuk karena terdapat beberapa titik, garis, dan bidang yang berada pada kedudukan tertentu sehingga dihasilkan bentuk suatu ruang misalnya kubus, kerucut, balok, dan sebagainya. Sebelum menyatakan kedudukan sebuah titik terhadap garis dan bidang, ada baiknya kita pahami terlebih dahulu pengertian dari masing-masing istilah dasar ini.#1 Titik
Titik merupakan istilah yang sudah tidak asing lagi bagi kita. Ditulis dengan noktah "." titik termasuk karakter yang sering kita gunakan dalam tulisan. Dalam kegiatan menulis, tanda titik umumnya digunakan untuk mengakhiri sebuah kalimat atau menyertai singkatan tertentu yang harus dibubuhi tanda titik. Lalu, apakah pengertian tersebut sama dengan titik dalam topik geometri?
Dalam kajian geometri, titik merupakan sebuah istilah yang digambarkan dengan menggunakan tanda noktah (.) yang kemudian dibubuhi nama titik tersebut. Titik memiliki kedudukan relatif terhadap garis dan bidang namun tidak terbatas terhadap ukuran. Artinya, benda langit seperti bintang yang jauh di angkas juga dapat dipandang sebagai kumpulan titik meskipun ukuran bintang tersebut sebenarnya lebih besar dari bumi.
Nama sebuah titik umumnya ditulis menggunakan huruf kapital (misalnya titik A, titik P, dan sebagainya) dan diletakkan di dekat titik tersebut. Nama tersebut berfungsi sebagai penjelas titik atau sebagai pengenal titik. Pemberian nama dimaksudkan agar kedudukan sebuah titik dapat dinyatakan dengan jelas terhadap garis atau bidang.
#2 Garis
Dari dua buah titik yang terpisah pada jarak tertentu dapat ditarik sebuah garis lurus yang biasanya akan diberi nama sesuai dengan nama titik yang dihubungkan. Misal titik yang dihubungkan adalah titik A dan B, maka garis yang terbentuk adalah garis AB. Panjang garis yang terbentuk sama dengan jarak terdekat antara titik A dan B.
Sebuah garis lurus dapat diperpanjang sesuai kebutuhan namun umumnya sebuah garis digambarkan sebagian saja sebagai wakil dari suatu garis. Sebuah garis memiliki ukuran panjang yang dinyatakan dengan satuan panjang (meter, cm, dan sebagainya) namun tidak memiliki ukuran lebar. Artinya, ketebalan sebuah garis umumnya diabaikan karena relatif tipis.
Selain dinyatakan berdasarkan titik-titik di kedua ujungnya yang dihubungkan, nama dari sebuah garis juga dapat dinyatakan dengan menggunakan nama yang mewakili garis tersebut. Untuk metode ini biasanya digunakan huruf kecil (misal garis k, garis l, garis g, dan sebagainya). Pada contoh gambar di atas, terdapat garis g atau disebut juga segmen garis AB.
#3 Bidang
Dari tiga atau lebih titik dapat dihasilkan sebuah bidang. Ketika tiga titik yang terpisah pada jarak tertentu dihubungkan dengan garis maka dapat dihasilkan sebuah bidang berbentuk segitiga. Tentu sja bentuk bidang yang dihasilkan bergantung pada posisi titik terhadap titik lainnya. Begitu pula pada bidang yang berbentuk persegi, bidang tersebut bisa saja diperoleh dari empat titik yang dihubungkan dengan garis lurus.
Bidang yang terbentuk dari hubungan tiga atau lebih titik seperti yang dijelaskan di atas umumnya diberi nama sesuai dengan nama titik-titik yang dihubungkan. Misalnya sebuah bidang berbentuk segitiga dihasilkan dari tiga buah titik yaitu titik A, B, dan C, maka bidang tersebut dapat dinamai sebagai bidang ABC.
Jika diperhatikan, sebuah bidang tidak hanya terbentuk dari adanya beberapa titik, tapi juga karena adanya beberapa garis yang saling dihubungkan. Dengan demikian, bidang juga dapat diartikan sebagai himpunan garis-garis yang anggotanya lebih dari dua garis. Misalnya bidang berbentuk segitiga terdiri dari tiga buah garis yang saling bertemu di kedua ujungnya.
Selain diberi nama berdasarkan titik-titik di sudut bidang tersebut, sebuah bidang biasanya juga dapat dinamai dengan menggunakan huruf yunani (α, β, γ) atau huruf kapital (H, U, V, W) yang diletakkan di salah satu sudut bidang tersebut.
B. Kedudukan Titik Terhadap Garis
Kedudukan titik terhadap sebuah garis dapat dinyatakan berdasarkan posisinya dari garis tersebut. Secara umum, terdapat dua kondisi yang menjelaskan kedudukan titik terhadap suatu garis yaitu berada tepat pada garis atau berada di luar garis.#1 Titik Terletak Pada Garis
Sebuah titik dikatakan terletak pada garis jika titik tersebut dilalui oleh garis atau titik tersebut bersentuhan tepat dengan segmen garis. Misalnya titik A dilalui oleh garis g, maka titik A dikatakan terletak pada garis. Pada contoh gambar di bawah, titik A dan titik B disebut terletak pada segmen garis g.
#2 Titik di Luar Garis
Jika sebuah titik tidak dilalui oleh sebuah garis, maka titik tersebut dikatakan berada di luar garis. Sebagai contoh, pada gambar kubus di bawah, titik A dan titik B dikatakan terletak di luar garis k, karena tidak dilalui oleh garis tersebut.
C. Kedudukan Titik Terhadap Bidang
Sama seperti kedudukan titik terhadap garis, kedudukan titik terhadap bidang juga dapat ditentukan berdasarkan posisi dan hubungan antara titik dengan bidang tersebut. Secara umum ada dua kondisi yang menjelaskan kedudukan titik terhadap bidang, yaitu terletak pada bidang dan terletak di luar bidang.#1 Titik Terletak Pada Bidang
Sebuah titik dikatakan terletak pada bidang jika titik tersebut dapat dilalui oleh bidang. Sebagai contoh perhatikan gambar kubus di atas. Pada gambar tersebut, titik P dikatakan terletak pada bidang α karena titik tersebut dilalui oleh bidang (titik P menempel tepat di bidang α).
#2 Titik di Luar Bidang
Jika sebuah titik tidak dapat dilalui oleh bidang, maka titik tersebut dikatakan berada di luar bidang. Sebagai contoh, pada gambar kubus di atas, titik Q disebut berada di luar bidang α karena bidang α tidak dapat melalui titik tersebut.
Demikianlah pembahasan singkat mengenai cara menyatakan kedudukan sebuah titik terhadap garis dan bidang di dalam suatu ruang tiga dimensi. Jika bahan belajar ini bermanfaat, bantu kami membagikannya kepada teman-teman anda melalui tombol share yang tersedia di bawah ini. Terimakasih.
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.