Nilai Maksimum Fungsi Tujuan Pertidaksamaan Linier dapat dilihat dengan menggambar grafik dari tiap-tiap kendala yang diberikan. Dengan mengetahui himpunan penyelesaian dari pertidaksamaan yang menjadi kendala, maka akan ditemukan himpunan penyelesaian yang memberikan nilai maksimum untuk fungsi tujuan tertentu.
Contoh soal :
Tentukanlah nilai maksimum dari fungsi tujuan 3x + 4y dengan kendala sebagai berikut : 2x + y ≤ 6, x + 2y ≤ 8, x ≥ 0, dan y ≥ 0.
Pembahasan :
Pertama-tama tentukan titik koordinat untuk masing-masing garis yang menjadi kendala :
Untuk 2x + y = 6
misal x = 0, maka y = 6 ---> (0,6)
misal y = 0, maka x = 3 ---> (3,0)
Untuk x + 2y = 8
misal x = 0, maka y = 4 ---> (0,4)
misal y = 0, maka x = 8 ---> (8,0)
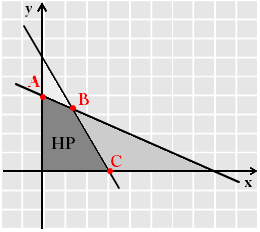
Kendala x ≥ 0 dan y ≥ 0 berarti nilai x dan y negatif tidak berlaku. Selanjutnya tentukan himpunan penyelesaian yang memenuhi kendala tersebut. Pada grafik di bawah ini terlihat bahwa garis 2x + y = 6 dan garis x + 2y = 8 berpotongan di titik B.
Karena kedua garis pada pertidaksamaan dalam soal ini adalah Kurang dari sama dengan (≤), maka himpunan penyelesaian untuk 2x + y ≤ 6 dan x + 2y ≤ 8 adalah daerah di bawah garis yaitu bagian yang diarsir berwarna abu-abu. Sedangkan himpunan penyelesaian gabungan yang memenuhi semua kendala adalah daerah yang diasrsir lebih gelap (bidang ABCO).
Selanjutnya, untuk mengetahui nilai maksimum fungsi tujuan, maka subsitusikan nilai x dan y pada titik A, B, dan C ke dalam fungsi tujuan. Untuk mengetahui koordinat titik B maka dapat digunakan metode eliminasi. Seperti yang terlihat pada grafik di atas, titik B merupakan perpotongan antara garis 2x + y = 6 dan garis x + 2y = 8, sehingga :
Substitusi nilai x dan y ke fungsi tujuan : Z = 3x + 4y
A (0,4) ----> Z = 3(0) + 4(4) = 16
B (4/3,10/3) ----> Z = 3(4/3) + 4(10/3) = 52/3 = 17,3
C (3,0) ----> Z = 3(3) + 4(0) = 9
Jadi nilai maksimum fungsi tujuan 3x + 4y dengan kendala 2x + y ≤ 6, x + 2y ≤ 8, x ≥ 0, dan y ≥ 0 adalah 17,3 yaitu pada titik B.
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.


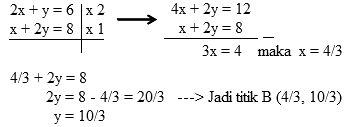
Terima kasih,,sangat membantu. :D
ReplyDeleteoke sama-sama umma, :)
Deletebermanfaat sekali, Terima kasih
ReplyDelete