Untuk menyelesaikan soal cerita program linear, dibutuhkan kemampuan analisis yang lebih tinggi dibanding soal program linear yang biasa. Hal ini karena pada soal cerita kita dituntut untuk mampu menyusun sendiri sistem persamaan atau pertidaksamaan linear yang sesuai dengan cerita untuk kemudian ditentukan himpunan penyelesaiannya. Tentu saja ketika kita keliru dalam menyusun persamaan atau pertidaksamaan linear, maka hasil yang kita peroleh juga keliru. Oleh karena itu, selain memahami konsep-konsep dasar program linear yang harus kita lakukan adalah banyak berlatih mengerjakan soal-soal cerita tentang perogram linear untuk memperkaya model soal.
Soal Cerita Program Linear
Soal 1 : Menentukan Harga Satuan
Aini, Nia, dan Nisa pergi bersama-sama ke toko buah. Aini membeli 2 kg apel, 2 kg anggur, dan 1 kg jeruk dengan harga Rp 67.000,00. Nia membeli 3 kg apel, 1 kg anggur, dan 1 kg jeruk dengan harga Rp 61.000,00. Nisa membeli 1 kg apel, 3 kg anggur, dan 2 kg jeruk dengan harga Rp. 80.000,00. Tentukan harga 1 kg apel, 1 kg anggur, dan 4 kg jeruk.
Pembahasan :
Dimisalkan : apel = x, anggur = y, jeruk = z
Dari soal, dapat disusun sistem persamaan linear sebagai berikut :
1). 2x + 2y + z = 67.000
2). 3x + y + z = 61.000
3). x + 3y + 2z = 80.000
Ditanya : x + y + 4z = ....?
Untuk menjawab pertanyaan seperti ini umumnya yang harus kita cari terlebih dahulu adalah harga satuan masing-masing barang.
Dari persamaan no 1 dan 2 diperoleh persamaan 4 :
Dari persamaan no 2 dan 3 diperoleh persamaan 5 :
Dari persamaan no 4 dan 5 diperoleh :
Jadi harga untuk 1 kg apel, 1 kg anggur, dan 4 kg jeruk adalah :
x + y + 4z = 12.000 + 18.000 + 4(7000) = Rp 58.000,00.
Soal 2 : Menentukan Harga Benda
Pada sebuah toko buku, Ana membeli 4 buku, 2 pulpen dan 3 pensil dengan
harga Rp 26.000,00. Lia membeli 3 buku, 3 pulpen, dan 1 pensil dengan
harga 21.000,00. Nisa membeli 3 buku dan 1 pensil dengan harga Rp.
12.000,00. Jika Bibah membeli 2 pulpen dan 3pensil, maka tentukan biaya
yang harus dikeluarkan oleh Bibah.
Pembahasan :
Dimisalkan : buku = x, pulpen = y, pensil = z
Dari soal, dapat disusun sistem persamaan linear sebagai berikut :
1). 4x + 2y + 3z = 26.000
2). 3x + 3y + z = 21.000
3). 3x + z = 12.000
Ditanya : 2y + 3z = ....?
Untuk menjawab pertanyaan seperti ini umumnya yang harus kita cari terlebih dahulu adalah harga satuan masing-masing barang. Karena yang ditanya harga 2y + 3z, maka kita hanya perlu mencari harga satuan y dan z.
Dari 3x + 3y + z = 21.000 dan 3x + z = 12.000, diperoleh harga satuan pulpen yaitu :
Selanjtunya, substitusi nilai y pada persamaan 1 dan 2 sebagai berikut :
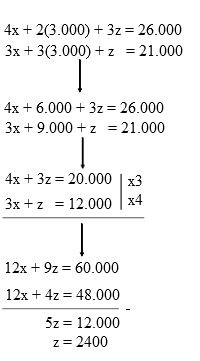
Jadi, harga 2 pulpen dan 3 pensil adalah :
2y + 3z = 2(3.000) + 3(2.400) = Rp 13.200,00.
Soal 3 : Menentukan Nilai Maksimum
Seorang pemilik toko sepatu ingin mengisi tokonya dengan sepatu
laki-laki paling sedikit 100 pasang dan sepatu wanita paling sedikit 150
pasang. Toko tersebut hanya dapat menampung 400 pasang sepatu.
Keuntungan setiap pasang sepatu laki-laki adalah Rp 10.000,00 dan keuntungan setiap pasang sepatu wanita adalah Rp 5.000,00. Jika banyaknya sepatu laki-laki tidak boleh melebihi 150 pasang, maka tentukanlah keuntungan terbesar yang dapat diperoleh oleh pemilik toko.
Pembahasan :
Pada soal ini, untuk mengetahui keuntungan terbesar maka yang menjadi fungsi tujuan atau fungsi objektifnya adalah keuntungan penjualan sepatu. Jadi fungsi tujuannya adalah :
F(x,y) = 10.000x + 5.000y
Dengan pemisalan :
sepatu laki-laki = x
sepatu perempuan = y
Sistem pertidaksamaan untuk soal tersebut adalah sebagai berikut :
x + y <= 400
100 => x <= 150
150 => y <= 250
Karena maksimum sepatu laki-laki hanya 150 pasang, maka maksimum sepatu perempuan = 400 - 150 = 250.
Dari sistem pertidaksamaan tersebut, maka diperoleh grafik sebagai berikut :
Dari grafik jelas telihat bahwa keuntungan maksimum berada pada titik pojok paling atas yaitu titik (150,250). Maka nilai maksimum dari fungsi tujuan F(x,y) = 10.000x + 5000y adalah :
F(150,250) = 150 (10.000) + 250 (5.000) = 2.750.000
Jadi, keuntungan terbesar yang dapat diperoleh pemilik toko adalah Rp 2.750.000,00.
Soal 4 : Menentukan Pendapatan Maksimum
Seorang pembuat kue mempunyai 8 kg
tepung dan 2 kg gula pasir. Ia ingin membuat dua macam kue yaitu kue
dadar dan kue apem. Untuk membuat kue dadar dibutuhkan 10 gram gula
pasir dan 20 gram tepung sedangkan untuk membuat sebuah kue apem
dibutuhkan 5 gram gula pasir dan 50 gram tepung. Jika kue dadar dijual
dengan harga Rp 300,00/buah dan kue apem dijual dengan harga Rp 500,00/buah, tentukanlah pendapatan maksimum yang dapat diperoleh
pembuat kue tersebut.
Pembahasan :
Untuk mengetahui pendapatan maksimum, maka terlebih dahulu kita menyusun sistem pertidaksamaan dan fungsi tujuan dari soal cerita tersebut. Karena yang ditanya pendapatan maksimum, maka tentu harga jual kue merupakan fungsi tujuan pada soal ini. Untuk menyusun sistem pertidaksamaan, yang perlu kita lakukan adalah menentukan variabel dan koefisiennya.
Misalkan :
Maka jumlah tepung, gula, dan harga jual merupakan koefisien. Agar lebih mudah, kita dapat memasukkan data yang ada pada soal ke dalam bentuk tabel seperti berikut :
Baca juga : Pembahasan Syarat Nilai Maksimum >>
Soal 6 : Menentukan Laba Maksimum Berdasarkan Fungsi Tujuan
Seorang pedagang menjual buah mangga dan pisang dengan menggunakan
gerobak. Pedagang tersebut membeli mangga dengan harga Rp 8.000,00/kg
dan pisang Rp 6.000,00/kg. Modal yang tersedia Rp 1.200.000,00 dan
gerobaknya hanya dapat menampung mangga dan pisang sebanyak 180 kg. Jika
harga jual mangga Rp 9.200,00/kg dan pisang Rp 7.000,00/kg, maka
tentukanlah laba maksimum yang diperoleh pedagang tersebut.
Aini, Nia, dan Nisa pergi bersama-sama ke toko buah. Aini membeli 2 kg apel, 2 kg anggur, dan 1 kg jeruk dengan harga Rp 67.000,00. Nia membeli 3 kg apel, 1 kg anggur, dan 1 kg jeruk dengan harga Rp 61.000,00. Nisa membeli 1 kg apel, 3 kg anggur, dan 2 kg jeruk dengan harga Rp. 80.000,00. Tentukan harga 1 kg apel, 1 kg anggur, dan 4 kg jeruk.
Pembahasan :
Dimisalkan : apel = x, anggur = y, jeruk = z
Dari soal, dapat disusun sistem persamaan linear sebagai berikut :
1). 2x + 2y + z = 67.000
2). 3x + y + z = 61.000
3). x + 3y + 2z = 80.000
Ditanya : x + y + 4z = ....?
Untuk menjawab pertanyaan seperti ini umumnya yang harus kita cari terlebih dahulu adalah harga satuan masing-masing barang.
Dari persamaan no 1 dan 2 diperoleh persamaan 4 :
Dari persamaan no 2 dan 3 diperoleh persamaan 5 :
Dari persamaan no 4 dan 5 diperoleh :
x + y + 4z = 12.000 + 18.000 + 4(7000) = Rp 58.000,00.
Soal 2 : Menentukan Harga Benda
Pembahasan :
Dimisalkan : buku = x, pulpen = y, pensil = z
Dari soal, dapat disusun sistem persamaan linear sebagai berikut :
1). 4x + 2y + 3z = 26.000
2). 3x + 3y + z = 21.000
3). 3x + z = 12.000
Ditanya : 2y + 3z = ....?
Untuk menjawab pertanyaan seperti ini umumnya yang harus kita cari terlebih dahulu adalah harga satuan masing-masing barang. Karena yang ditanya harga 2y + 3z, maka kita hanya perlu mencari harga satuan y dan z.
Dari 3x + 3y + z = 21.000 dan 3x + z = 12.000, diperoleh harga satuan pulpen yaitu :
Selanjtunya, substitusi nilai y pada persamaan 1 dan 2 sebagai berikut :
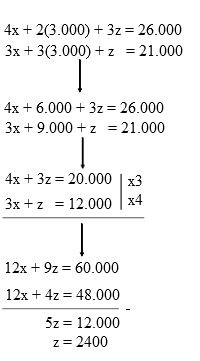
Jadi, harga 2 pulpen dan 3 pensil adalah :
2y + 3z = 2(3.000) + 3(2.400) = Rp 13.200,00.
Soal 3 : Menentukan Nilai Maksimum
Keuntungan setiap pasang sepatu laki-laki adalah Rp 10.000,00 dan keuntungan setiap pasang sepatu wanita adalah Rp 5.000,00. Jika banyaknya sepatu laki-laki tidak boleh melebihi 150 pasang, maka tentukanlah keuntungan terbesar yang dapat diperoleh oleh pemilik toko.
Pembahasan :
Pada soal ini, untuk mengetahui keuntungan terbesar maka yang menjadi fungsi tujuan atau fungsi objektifnya adalah keuntungan penjualan sepatu. Jadi fungsi tujuannya adalah :
F(x,y) = 10.000x + 5.000y
Dengan pemisalan :
sepatu laki-laki = x
sepatu perempuan = y
Sistem pertidaksamaan untuk soal tersebut adalah sebagai berikut :
x + y <= 400
100 => x <= 150
150 => y <= 250
Karena maksimum sepatu laki-laki hanya 150 pasang, maka maksimum sepatu perempuan = 400 - 150 = 250.
Dari sistem pertidaksamaan tersebut, maka diperoleh grafik sebagai berikut :
 |
| Sistem pertidaksamaan linear |
Dari grafik jelas telihat bahwa keuntungan maksimum berada pada titik pojok paling atas yaitu titik (150,250). Maka nilai maksimum dari fungsi tujuan F(x,y) = 10.000x + 5000y adalah :
F(150,250) = 150 (10.000) + 250 (5.000) = 2.750.000
Jadi, keuntungan terbesar yang dapat diperoleh pemilik toko adalah Rp 2.750.000,00.
Soal 4 : Menentukan Pendapatan Maksimum
Pembahasan :
Untuk mengetahui pendapatan maksimum, maka terlebih dahulu kita menyusun sistem pertidaksamaan dan fungsi tujuan dari soal cerita tersebut. Karena yang ditanya pendapatan maksimum, maka tentu harga jual kue merupakan fungsi tujuan pada soal ini. Untuk menyusun sistem pertidaksamaan, yang perlu kita lakukan adalah menentukan variabel dan koefisiennya.
Bahan yang tersedia:
Tepung = 8 kg = 8000 g
Gula = 2 kg = 2000 g
Misalkan :
kue dadar = x
kue apem = y
Maka jumlah tepung, gula, dan harga jual merupakan koefisien. Agar lebih mudah, kita dapat memasukkan data yang ada pada soal ke dalam bentuk tabel seperti berikut :
Dari tabel di atas dapat disusun sistem pertidaksamaan sebagai berikut :
20x + 50y = 800 ---> 2x + 5y <= 800
10x +5y = 2000 ---> 2x + y <= 400
x >= 0 dan y >= 0
dengan fungsi tujuan f(x,y) = 300x + 500y
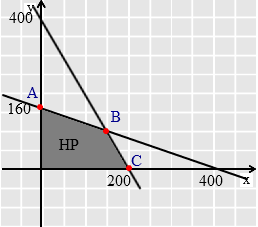
Kemudian gambarkan sistem pertidaksamaan yang sudah disusun dalam grafik.
Untuk garis 2x + 5y = 800
x = 0, y = 160 ---> (0, 160)
y = 0, x = 400 ---> (400, 0)
Untuk garis 2x + y = 400
x = 0, y = 400 ---> (0, 400)
y = 0, x = 200 ---> (200, 0)
Titik B merupakan titik potong garis 2x + 5y = 800 dengan garis 2x + y = 400
2x + y = 400
y = 400 - 2x
Dengan metode substitusi :
2x + 5y = 800
2x + 5(400 - 2x) = 800
2x + 2000 - 10x = 800
-8x = -1200
x = 150
Karena x = 150, maka :
y = 400 - 2x
y = 400 - 2(150)
y = 400 - 300
y = 100
Dengan demikian titik B (150, 100)
Selanjutnya substitusikan titik A, B, dan C ke fungsi tujuan :
A(0, 160) ---> F(x,y) = 300(0) + 500(160) = 80.000
B(150, 100) ---> F(x,y) = 300(150) + 500(100) = 95.000
C(200, 0) ---> F(x,y) = 300(200) + 500(0) = 60.000
x = 0, y = 160 ---> (0, 160)
y = 0, x = 400 ---> (400, 0)
Untuk garis 2x + y = 400
x = 0, y = 400 ---> (0, 400)
y = 0, x = 200 ---> (200, 0)
 |
| Sistem pertidaksamaan linear |
Titik B merupakan titik potong garis 2x + 5y = 800 dengan garis 2x + y = 400
2x + y = 400
y = 400 - 2x
Dengan metode substitusi :
2x + 5y = 800
2x + 5(400 - 2x) = 800
2x + 2000 - 10x = 800
-8x = -1200
x = 150
Karena x = 150, maka :
y = 400 - 2x
y = 400 - 2(150)
y = 400 - 300
y = 100
Dengan demikian titik B (150, 100)
A(0, 160) ---> F(x,y) = 300(0) + 500(160) = 80.000
B(150, 100) ---> F(x,y) = 300(150) + 500(100) = 95.000
C(200, 0) ---> F(x,y) = 300(200) + 500(0) = 60.000
Jadi, pendapatan maksimum yang bisa diperoleh pedagang kue itu adalah Rp 95.000,00.
Soal 5 : Menentukan Syarat Nilai Maksimum
Menjelang hari raya Idul Adha, Pak
Mahmud hendak menjual sapi dan kerbau. Harga seekor sapi dan kerbau di
Medan berturut-turut Rp 9.000.000,00 dan Rp 8.000.000,00. Modal yang
dimiliki pak Mahmud adalah Rp 124.000.000,00. Pak Mahmud menjual sapi
dan kerbau di Aceh dengan harga berturut-turut Rp 10.300.000,00 dan Rp
9.200.000,00. Kandang yang ia miliki hanya dapat menampung tidak lebih
dari 15 ekor. Agar mencapai keuntungan maksimum, tentukanlah banyak sapi
dan kerbau yang harus dibeli pak Mahmud.Soal 5 : Menentukan Syarat Nilai Maksimum
Baca juga : Pembahasan Syarat Nilai Maksimum >>
Soal 6 : Menentukan Laba Maksimum Berdasarkan Fungsi Tujuan
Baca juga : Pembahasan Laba Maksimum >>
Soal 7 : Menentukan Titik Optimum Fungsi Tujuan
Biaya produksi tipe lux dan tipe sport masing-masing adalah Rp 40.000 dan Rp 28.000 per unit. Untuk satu periode produksi, perusahaan menggunakan paling sedikit 120 batang kayu jati dan 24 kaleng cat pernis. Bila perusahaan harus memproduksi lemari tipe lux paling sedikit 2 buah dan tipe sport paling sedikit 4 buah, tentukan banyak lemari tipe lux dan tipe sport yang harus diproduksi agar biaya produksinya minimum.
Baca juga : Pembahasan Titik Optimum Fungsi Tujuan >>
Soal 8 : Menentukan Nilai Minimum Fungsi Tujuan
Soal 9 : Menentukan Nilai Minimum Fungsi Objektif
Baca juga : Pembahasan Nilai Minimum Fungsi Objektif >>
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.
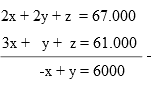
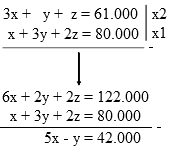
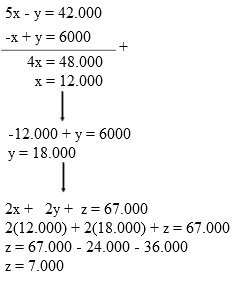


sebuah industri keramik membuat 2 jenis produk unggulan A dan B, untuk menghasilkan satu buah jenis produk A diperlukan waktu pengerjaan 1 jam dan bahan baku 3kg. waktu pengerjaandan bahan baku yang tersedia masing-masing 40 jam dan 120 kg. keuntungan tiap unit A dan B masing-masing 40 dan 50. di tanya: berapakah jumlah masing-masing keramik yang harus dibuat agar keuntungan yang diraih mencapai nilai maksimal?
ReplyDeleteuntuk jenis B, waktu dan bahan baku yg dibutuhkan berapa?
ReplyDeletethanks
ReplyDeletePermisi min yang nomer 4 itu X=150 dan Y=100 jadi titik B f(150,100) bukan (100,150)
ReplyDeleteThanks so much Ririf!! Trimakasih atas koreksinya.
DeleteAkan segera diperbaiki.
Salam kenal.
wah super sekali, butuh berapa hari mas untuk membuat artikel sepanjang ini? o ya gimana kabar masalah blogspot.co.id nya sudh ada informasi belum, wah bener-bener jadi tekor ne haha..
ReplyDeleteWah gak ingat mas Imam. Yg pasti dulu lama banget bisa berjam-jam. Belum ada kbr tuh mas mgkin senin. Ya, sabar ajalah mas kalau memang rezeki pasti gak kemana. Yg penting optimis aja.
Delete