Seperti contoh-contoh lain yang telah dibahas di blog ini, langkah-langkah untuk menentukan nilai maksimum fungsi tujuan dengan garfik adalah sebagai berikut :
- Tentukan titik potong garis kendala yang diberikan terhadap sumbu x dan sumbu y untuk menentukan titik kordinat.
- Gambarkan garis kendala ke dalam grafik sesuai dengan titik koordinat yang telah diperoleh pada langkah 1.
- Tentukan daerah himpunan penyelesaian yang sesuai dengan tanda pertidaksamaan. Jika masih bingung bagaimana menentukan daerah himpunan penyelesaian, anda dapat membaca postingan Menentukan Himpunan Penyelesaian Sistem Pertidaksamaan Linear.
- Tentukan titik-titik pojok yang berada dalam daerah himpunan penyelesaian dan substitusi nilainya ke dalam fungsi objektif atau fungsi tujuan untuk melihat titik mana yang menghasilkan nilai maksimum. Untuk tahap ini, kita juga dapat menggunakan Garis Selidik.
Contoh soal :
- Apabila x, y anggota bilangan real terletak pada himpunan penyelesaian
sistem pertidaksamaan x ≥ 0; y ≥ 0; 2x + y ≤ 8; dan x + 3y ≤ 9 maka tentukanlah nilai maximum fungsi sasaran x + 2y pada
himpunan penyelesaian tersebut.
Pembahasan :
Tentukan titik potong masing-masing kendala terhadap sumbu x dan sumbu y sebagai berikut :
Untuk 2x + y = 8
misal x = 0 , y = 8 → (0,8)
misal y = 0 , x = 4 → (4,0)
Untuk x + 3y = 9
misal x = 0 , y = 3 → (0,3)
misal y = 0 , x = 9 → (9,0)
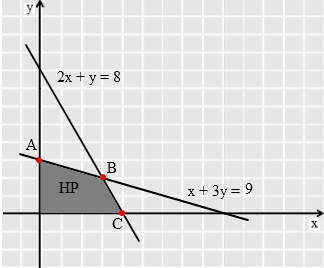
Selanjutnya, gambarkan garis tersebut ke dalam grafik seperti berikut :
Setelah itu tentukan daerah himpunan penyelesaiannya. Karena pertidaksamaan bertanda lebih kecil dari sama dengan (≤), maka daerah himpunan penyelesaiannya adalah daerah di bawah/kiri garis.
Dari gambar dapat dilihat bahwa ada tiga titik pojok yaitu titik A, B, dan C. Titik A dan C dapat dengan mudah ditentukan karena merupakan titik potong terhadap sumbu y dan sumbu x. Titik B merupakan perpotongan antara garis 2x + y = 8 dan x + 3y = 9. Dari grafik dapat dilihat bahwa kedua garis itu berpotongan tepat di titik (3,2).
Langkah terakhir, substitusi nilai x dan y dari masing-masing titik pojok ke fungsi tujuan F(x,y) = x + 2y sebagai berikut :
A(0,3) → F(0,3) = 0 + 2(3) = 6
B(3,2) → F(3,2) = 3 + 2(2) = 7 → maksimum.
C(4,0) → F(4,0) = 4 + 2(0) = 4
Jadi nilai maksimum fungsi tujuannya adalah 7 yaitu pada titik B.
- Jika diketahui A = x + y dan B = 5x + y, maka tentukanlah jumlah nilai maksimum
dari A dan B pada sistem pertidaksamaan x ≥ 0; y ≥ 0; x + 2y ≤ 12; 2x + y ≤ 12.
Pembahasan :
Tentukan titik potong masing-masing kendala terhadap sumbu x dan sumbu y sebagai berikut :
Untuk x + 2y = 12
misal x = 0 , y = 6 → (0,6)
misal y = 0 , x = 12 → (12,0)
Untuk 2x + y = 12
misal x = 0 , y = 12 → (0,12)
misal y = 0 , x = 6 → (6,0)
Selanjutnya, gambarkan garis tersebut ke dalam grafik seperti di atas dan tentukan daerah himpunan penyelesaiannya.
Dari gambar dapat dilihat bahwa ada tiga titik pojok yaitu titik A, B, dan C. Titik A dan C dapat dengan mudah ditentukan karena merupakan titik potong terhadap sumbu y dan sumbu x. Titik B merupakan perpotongan antara garis x + 2y = 12 dan 2x + y = 12. Dari grafik dapat dilihat bahwa kedua garis itu berpotongan tepat di titik (4,4) → pada gambar di atas, 1 kotak mewakili 2 satuan.
Langkah terakhir, substitusi nilai x dan y dari masing-masing titik pojok ke fungsi tujuan A(x,y) = x + y dan B(x,y) = 5x + y sebagai berikut :
A(0,6) → A(0,6) = 0 + 6 = 6
B(4,4) → A(4,4) = 4 + 4 = 8 → maksimum.
C(6,0) → A(6,0) = 6 + 0 = 6
A(0,6) → B(0,6) = 5(0) + 6 = 6
B(4,4) → B(4,4) = 5(4) + 4 = 24
C(6,0) → B(6,0) = 5(6) + 0 = 30 → maksimum.
Jadi jumlah nilai maksimum fungsi tujuan A + B = 8 + 30 = 38
- Tentukan nilai maksimum dari fungsi tujuan 4x + 3y dari sistem
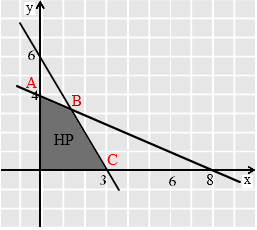
pertidaksamaan yang memiliki himpunan penyelesaian seperti gambar di bawah ini.
Pembahasan :
Pada gambar di atas, daerah yang diarsir (berwarna gelap) merupakan daerah himpunan penyelesaian sistem pertidaksamaan. Daerah tersebut memiliki 4 titik pojok atau titik sudut yang di antaranya adalah titik (0,0). Karena kita akan mencari nilai maksimum fungsi objektif atau fungsi tujuan, maka titik (0,0) tentu tidak memenuhi.
Dari gambar di atas, terdapat 3 titik pojok yang salah satunya menghasilkan nilai maksimum jika disubstitusikan ke fungsi tujuan, yaitu titik A, B, dan C. Sekarang yang harus dilakukan adalah menentukan titik-titik tersebut. Titik A dan C dapat dengan mudah diketahui karena merupakan titik potong garis terhadap sumbu x dan sumbu y. Adapun titik A (0,4) dan titik C (3,0). Sementara itu, titik B merupakan perpotongan antara dua garis yang belum kita ketahui persamaan garisnya. Oleh karena itu, untuk mengetahui titik B sebaiknya kita tentukan terlebih dahulu persamaan garis yang saling berpotongan di titik itu dengan cara sebagai berikut :
Sesuai dengan skema dan rumus di atas, maka :untuk a = 4, b = 84x + 8y = 32 → x + 2y = 8
untuk a = 6, b = 3
6x + 3y = 18 → 2x + y = 6
Titik B (titik potong antara x + 2y = 8 dan 2x + y = 6) dapat dicari dengan metode eliminasi.
Selanjutnya substitusi masing-masing titik (A, B, dan C) ke fungsi tujuan f(x,y) = 4x + 3y.
A (0,4) → f(x,y) = 4(0) + 3(4) = 12
B (4/3, 10/3) → f(x,y) = 4(4/3) + 3(10/3) = 46/3 = 15,3
C (3,0) → f(x,y) = 4(3) + 3(0) = 12
Jadi nilai maksimum fungsi tujuan dengan kendala seperti gambar di atas adalah 15,3 yaitu pada titik B.
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.





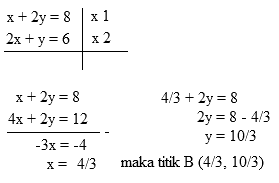
0 comments :
Post a Comment