Jika untuk mencari himpunan penyelesaian suatu pertidaksamaan linear dapat digunakan metode grafik, maka sebaliknya kita dapat menentukan atau menyusun sistem pertidaksamaan yang memiliki daerah himpunan penyelesaian seperti pada grafik.
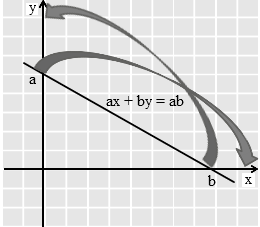
Caranya sangat sederhana. Pada prinsipnya, yang harus kita lakukan adalah melihat titik potong garis-garis pada grafik terhadap sumbu x dan sumbu y kemudian menyusun persamaan garisnya. Untuk tujuan praktis, kita dapat menggunakan rumus berikut :
Caranya sangat sederhana. Pada prinsipnya, yang harus kita lakukan adalah melihat titik potong garis-garis pada grafik terhadap sumbu x dan sumbu y kemudian menyusun persamaan garisnya. Untuk tujuan praktis, kita dapat menggunakan rumus berikut :
ax + by = ab
Setelah persamaan garisnya kita peroleh, maka selanjutnya adalah melihat himpunan penyelesaian (HP) yang tertera di grafik.
Jika garis berada di kuadran pertama dan kuadran keempat ( sebelah kanan) seperti pada contoh, maka pertidaksamaannya dapat ditentukan dengan cara berikut :
- Kurang dari (<) → HP terletak di bawah garis, garis lurus berupa garis putus-putus
- Lebih dari (>) → HP terletak di atas garis, garis lurus berupa garis putus-putus
- Kurang dari sama dengan (≤) → HP terletak di bawah garis, garis lurus berupa garis utuh
- Lebih dari sama dengan (≥) → HP terletak di atas garis, garis lurus berupa garis utuh
Contoh soal:
Tentukan sistem pertidaksamaan yang memiliki daerah himpunan penyelesaian seperti gambar di bawah ini.
Pembahasan:
Untuk a = 6, b = 3
maka persamaan garisnya 6x + 3y = 18 → 2x + y = 6
Untuk a = 4, b =6
maka persamaan garisnya 4x + 6y = 24 → 2x + 3y = 12
Untuk a = 2, b = tak hingga
maka persamaan garisnya 2x + ∞y = 2∞ → y = 2
Lihat Himpunan Penyelesaiannya :
- Di bawah garis 2x + 3y = 12 → 2x + 3y ≤ 12
- Di atas garis 2x + y = 6 → 2x + y ≥ 6
- Di atas garis y = 2 → y ≥ 2
2x + 3y ≤ 12, 2x + y ≥ 6, dan y ≥ 2.
Note :
Cara di atas hanya berlaku untuk grafik pada kuadran I dan IV. Untuk grafik sebelah kiri (kuadran II dan III), maka gunakan aturan kebalikannya, sebagai berikut :
- Kurang dari (<) → HP terletak di atas garis, garis lurus berupa garis putus-putus
- Lebih dari (>) → HP terletak di bawah garis, garis lurus berupa garis putus-putus
- Kurang dari sama dengan (≤) → HP terletak di atas garis, garis lurus berupa garis utuh
- Lebih dari sama dengan (≥) → HP terletak di bawah garis, garis lurus berupa garis utuh
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.





maksudnya di atas garis di bawah garis itu gimana ?
ReplyDeleteKalau pd pembahasan ini maksudnya daerah yg diarsir. Yang diarsir itu daerah himpunan penyelesainnya mksudnya semua nilai x atau y yang berada di daerah itu memenuhi persamaannya. Di atas atau di bawah tergantung letak garis dan daerah arsiran.
Deletejadi penentuan nilai x dan y nya menggunakan titik uji (0,0) ? apa harus menggunakan titik uji itu?
ReplyDelete