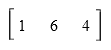Matriks adalah susunan kumpulan bilangan yang diatur dalam baris dan kolom berbentuk persegi panjang. Matriks dicirikan dengan elemen-elemen penyusun yang diapit oleh tanda kurung siku [ ] atau tanda kurung biasa ( ). Ukuran sebuah matriks dinyatakan dalam satuan ordo, yaitu banyaknya baris dan kolom dalam matriks tersebut. Ordo merupakan karakteristik suatu matriks yang menjadi patokan dalam operasi-operasi antar matriks.
Memahami ordo matriks merupakan hal yang penting karena cukup banyak terjadi kesalahan dalam mengerjakan soal-soal matriks yang disebabkan oleh kekeliruan dalam memahami ordo matriks. Ketika seorang murid mengartikan ordo secara terbalik yaitu kolom dikali baris tentu hasilnya akan sangat berbeda. Matriks umumnya disimbolkan seperti berikut ini :
Amxn
Memahami ordo matriks merupakan hal yang penting karena cukup banyak terjadi kesalahan dalam mengerjakan soal-soal matriks yang disebabkan oleh kekeliruan dalam memahami ordo matriks. Ketika seorang murid mengartikan ordo secara terbalik yaitu kolom dikali baris tentu hasilnya akan sangat berbeda. Matriks umumnya disimbolkan seperti berikut ini :
Amxn
A = nama matriks
m = banyaknya baris
n = banyaknya kolom
m x n = ordo matriks
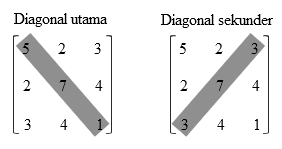
Pada gambar di atas, diagonal utama merupakan garis miring yang dibentuk oleh elemen matriks 5, 7, dan 1 sedangkan diagonal sekunder merupakan garis miring yang dibentuk oleh elemen matriks 3, 7, dan 3.
Jenis-jenis Matriks
Untuk mempermudah mempelajari jenis-jenis matriks, ada baiknya kita telebih dahulu memahami pengertian diagonal dalam matriks. Pada matriks terdapat dua dioganal, yaitu diagonal utama dan diagonal skunder. Pengertian diagonal utama dan diagonal skunder dapat dilihat dari gambar berikut ini :Pada gambar di atas, diagonal utama merupakan garis miring yang dibentuk oleh elemen matriks 5, 7, dan 1 sedangkan diagonal sekunder merupakan garis miring yang dibentuk oleh elemen matriks 3, 7, dan 3.
Berdasarkan Jumlah Baris dan Kolom
Berdasarkan jumlah baris dan kolomnya, secara umum matriks dibagi menjadi lima jenis, yaitu :
Bila matriks A dan B dinyatakan sama, maka :
A = B
Berlaku :
a = p; b = q ; c = r;
d = s; e = t; f = u
g = v; h = w; l = x
"Rahasia kecerdasan bukan terletak pada mempelajari apa yang disenangi, tetapi pada menyenangi apa yang sedang dipelajari."
- Matriks persegi
- Matriks baris
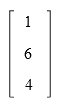
- Matriks kolom
- Matriks mendatar
- Matriks tegak
Berdasarkan Pola Elemennya
Berdasarkan pola elemen-elemennya, matriks dibagi menjadi beberapa jenis, yaitu :- Matriks nol
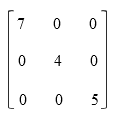
- Matriks diagonal
- Matriks identitas
- Matriks segitigaMatriks segitiga terdiri dari dua jenis yaitu matriks segitiga atas dan matriks segitiga bawah. Matriks segitiga atas merupakan matriks yang elemen-elemen di bawah diagonal utamanya bernilai nol. Matriks segitiga bawah merupakan matriks yang elemen-elemen di atas diagonal utamanya bernilai nol.
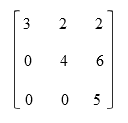
Matriks segitiga atas 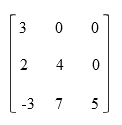
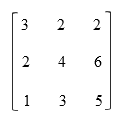
Matriks segitiga bawah - Matriks simetrisMatriks simetris adalah matriks yang elemen-elemen di bawah dan di atas diagonal utamanya simetris. Dengan kata lain, elemen pada sel mn sama dengan elemen pada sel nm, misalnya elemen pada sel 12 sama dengan elemen pada sel 21. Pada gambar di bawah dapat dilihat bahwa elemen pada sel 21 sama dengan elemen pada sel 12 yaitu 2.
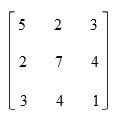
Matriks simetris 3 x 3 - Matriks skalarMatriks skalar adalah matriks yang elemen-elemen pada diagonal utamanya sama dan elemen lain bernilai nol.
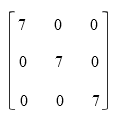
Matriks skalar 3 x 3
Kesamaan Matriks
Dua atau lebih matriks dikatakan sama bila memiliki ordo sama dan memiliki komponen yang sama pada setiap selnya. Dengan kata lain, matriks-matriks tersebut adalah matriks yang sama hanya berbeda nama.Bila matriks A dan B dinyatakan sama, maka :
A = B
Berlaku :
a = p; b = q ; c = r;
d = s; e = t; f = u
g = v; h = w; l = x
"Rahasia kecerdasan bukan terletak pada mempelajari apa yang disenangi, tetapi pada menyenangi apa yang sedang dipelajari."
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.