Model soal tentang teori peluang yang sering muncul dalam ujian nasional bidang studi matematika antara lain : menentukan peluang munculnya suatu anggota kelompok secara berdampingan dalam suatu kejadian P(k), menentukan peluang munculnya jumlah mata dadu tertentu, menentukan peluang kejadian saling bebas P(A∩B), menentukan banyak cara yang mungkin dari suatu kejadian, dan lain sebagainya. Berikut beberapa soal ujian nasional tentang teori peluang yang dihimpun dari beberapa naskah soal UN.
Kumpulan Soal
- (Ujian Nasional 2008/2009)Di sebuah kelas terdiri dari 30 orang siswa. Pada kelas tersebut akan dipilih 3 orang sebagai pengurus kelas yang menjabat sebagai ketua kelas, sekretaris, dan wakil ketua. Banyaknya cara memilih yang mungkin adalah ...
A. 24.360
B. 24.630
C. 42.360
D. 42.630
E. 46.230
Pembahasan :
Pemilihan ketua kelas, sekeretaris, dan wakil ketua mengikuti aturan permutasi yaitu memperhatikan urutan. Dengan kata lain jika tiga siswa misalnya A, B, dan C dipilih menjadi pengurus kelas dengan susunan A sebagai ketua, B sebagai wakil, dan C sebagai sekeretaris akan berbeda dengan susunan B sebagai ketua, C sebagai wakil, dan A sebagai sekretaris (ABC ≠ BCA).
Banyak cara memilih ketua, wakil ketua, dan sekretaris dari 30 siswa merupakan permutasi 3 unsur dari 30 unsur yang tersedia. Berdasarkan konsep permutasi dapat dihitung dengan rumus :
nPr = n! / (n - r)! ; r ≤ n
dengan :
nPr = banyak permutasi r unsur dari n unsur yang tersedia.
r = banyak unsur yang dipilih
n = banyak unsur yang tersedia
Maka :
nPr = n! / (n - r)!
30P3 = 30! / (30 - 3)!
30P3 = 30! / 27!
30P3 = (30 x 29 x 28 x27!) /27!
30P3 = 30 x 29 x 28
30P3 = 24.360 ---> opsi A.
- (Ujian Nasional 2008/2009)Dari perangkat kartu bridge diambil dua kartu sekaligus secara acak. Peluang yang terambil dua kartu king adalah ...
A. 1/221
B. 1/13
C. 4/221
D. 11/221
E. 8/663
Pembahasan :
Peluang terambilnya dua kartu king mengikuti aturan kombinasi yaitu pengelompokkan unsur tanpa memperhatikan urutan. Banyakya kombinasi yang terjadi dapat dihitung dengan rumus :
nCr = n! / {r! (n - r)!}
dengan :
nCr = banyaknya kombinasi r unsur dari n unsur yang tersedia
n = banyak unsur yang tersedia
r = banyak unsur yang diambil
Peluang terambilnya 2 kartu king dari total 4 kartu king
nCr = n! / {r! (n - r)!}
4C2 = 4! / {2! (4 - 2)!}
4C2 = 4! / (2! . 2!)
4C2 = 4 x 3 x2!/ 2 x 1 x2!
4C2 = 12 / 2 = 6
Peluang terambilnya 2 kartu king dari total 52 kartu bridge
52C2 = 52! / {2! (52 - 2)!}
52C2 = 52! / (2! . 50!)
52C2 = 52 x 51 x50!/ 2 x 1 x50!
52C2 = 1326
Maka peluang terambilnya dua kartu king adalah :
P(k) = 4C2 / 52C2
P(k) = 6 / 1326
P(k) = 1/221 ---> opsi A.
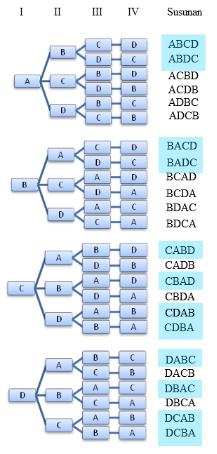
- (Ujian Nasional 2005/2006)A, B, C, dan D akan berfoto bersama secara berdampingan. Peluang A dan B selalu berdampingan adalah ...
A. 1/12
B. 1/6
C. 1/3
D. 1/2
E. 2/3
Pembahasan :
Karena ada 4 orang yang akan berfoto, maka anggaplah akan ada 4 ruang yang akan diisi oleh mereka dengan cara yang berbeda.
Misal :
Tempat → I II III IV
Cara penempatan → 4 3 2 1
Berdasarkan aturan pencacahan, maka banyak susunan yang terjadi adalah :
banyak susunan = 4 x 3 x 2 x 1 = 24 cara.
Dengan menggunakan diagram pohon seperti di atas, maka diperoleh banyak susunan di mana A dan B selalu berdampingan adalah 12. Berdasarkan teori peluang, peluang suatu kejadian adalah :
n(k)
P(k) = ——
n(s)
dengan :
P(k) = peluang kejadian
n(k) = banyak kejadian
n(s) = banyak kejadian semesta
Pada soal ini diketahui :
n(k) = 12
n(s) = 24
Maka peluang A dan B selalu berdampingan adalah :
P(k) = 12/24 = 1/2 ---> opsi D
- (Ujian Nasional 2006/2007)Dalam kantong I terdapat 5 kelereng merah dan 3 kelereng putih, dalam kantung II terdapat 4 kelereng merah dan 6 kelereng hitam. Dari setiap kantong diambil satu keelreng secara acak. Peluang terambilnya kelereng putih dari kantong I dan kelereng hitam dari kantong II adalah ...
A. 39/40
B. 9/13
C 1/2
D 9/20
E. 9/40
Pembahasan :
Kanong I = 5 kelereng merah, 3 kelereng putih
Kantong II = 4 kelereng merah, 6 kelereng hitam
Misalkan :
A = kejadian terambilnya kelereng putih dari kantong I
P(A) = peluang terambilnya kelereng putih dari kantong I
B = kejadian terambilnya keleeng hitam dari kantong II
P(B) = peluang terambilnya kelereng hitam dari kantung II
Peluang terambilnya kelereng putih dari kantong I dan kelereng hitam dari kantong II merupakan peluang kejadian saling bebas yang dapat dihitung dengan rumus :
P(A∩B) = P(A) . P(B)
Pada kantung I :
n(A) = 3
n(s) = 3 + 5 = 8
P(A) = 3/8
Pada kantong II :
n(B) = 6
n(s) = 6 + 4 = 10
P(B) = 6/10
Maka peluang terambilnya kelereng putih dari kantong I dan kelereng hitam dari kantong II adalah :
P(A∩B) = P(A) . P(B)
P(A∩B) = 3/8 . 6/10
P(A∩B) = 18/80
P(A∩B) = 9/40 ---> opsi E.
- (Ujian Nasional 2007/2008)Dua buah dadu dilempar undi secara bersamaan sebanyak satu kali. Peluang kejadian muncul jumlah mata dadu 9 atau 11 adalah ...
A. 1/2
B. 1/4
C. 1/6
D. 1/8
E. 1/12
Pembahasan :
Misalkan :
A = kejadian muncul jumlah mata dadu 9
P(A) = peluang muncul jumlah mata dadu 9
B = kejadian muncul jumlah mata dadu 11
P(B) = peluang muncul jumlah mata dadu 11
A∪B = peluang muncul jumlah mata dadu 9 atau 11
Peluang kejadian muncul jumlah mata dadu 9 atau mata dadu 11 merupakan peluang gabungan dua kejadian yang berdasarkan teori peluang dapat dihitung dengan menggunakan rumus di bawah ini :
P(A∪B) = P(A) + P(B)
Bila dicari berdasarkan tabel ataupun diagram pohon, banyak kejadian semesta dari pelemparan dua dadu adalah 36. Dengan begitu diperoleh peluang munculnya jumlah mata dadu 9 dan peluang munculnya mata dadu 11 masing-masing sebagai berikut :
P(A) = 4/36 ---> n(A) = 4 yaitu (6+3), (3+6), (4 + 5), dan (5 + 4).
P(B) = 2/36 ---> n(B) = 2 yaitu (5 + 6) dan (6 + 5).
Maka :
P(A∪B) = P(A) + P(B)
P(A∪B) = 4/36 + 2/36
P(A∪B) = 6/36
P(A∪B) = 1/6 ---> opsi C.
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.
Permisi minta bantuannya dong !
ReplyDeleteDalam suatu kotak terdapat 7 kelereng merah dan 3 kelereng putih. Tiga kelereng diambil satu persatu secara acak tanpa pengembalian. jika pengambilan dilakukan sebanyak 336 kali, maka frekuensi harapan terambilnya tiga kelereng merah adalah ...
*minta penjelasan serta rinciannya :)
Karena diambil 3 tanpa pengembalian, maka ada tiga keadaan :
DeletePengambilan kelereng pertama :
jumlah kelereng = 10
merah = 7
peluang terambil merah = P(m1) = 7/10.
Pengambilan kelerenga kedua :
jumlah kelereng = 9 karena sudah diambil 1.
merah = 6
Peluang terambil merah : P(m2) = 6/9
Pengambilan kelereng ketiga :
jumlah kelereng = 8 karena dikurang 2.
merah = 5
Peluang terambil merah = 5/8
Peluang terambil 3 merah :
P(m1 ∩ m2 ∩ m3) = 7/10 (6/9) (5/8) = 210/720
Frekuens harapan terambil tiga kelereng merah :
F(n) = n P(m1 ∩ m2 ∩ m3)
F(336) = 336 (210/720) = 98
Oh terima kasih banyak atas penjelasannya ka ..
Delete