RUMUS PENJUMLAHAN DAN PERKALIAN TRIGONOMETRI

Analisis tentang trigonometri pada dasarnya berlandaskan pada karakteristik sudut-sudut istimewa yang memberikan kontribusi lebih lanjut untuk menentukan nilai trigonometri sudut-sudut lain. Oleh karena itu, sangat penting untuk memahami konsep dasar trigonometri.


Untuk tingkat SMA ada baiknya jika kita menghafal nilai perbandingan trigonometri sudut-sudut istimewa karena hal itu akan sangat membantu kita dalam memahami persoalan trigonometri yang lebih kompleks.

Dengan mengembangkan prinsip-prinsip perbandingan trigonometri sudut berelasi dan sudut-sudut istimewa, maka dihasilkan rumus-rumus yang menjadi identitas trigonometri.

Rumus dasar trigonometri dapat dilihat pada gambar dan penjabaran di bawah ini :

Rumus sin, cos, dan tan
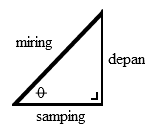
sin θ = sisi depan  → demi
            sisi miring

cos θ = sisi samping  → sami
             sisi miring

tan θ =   sisi depan      → desa   
             sisi samping

Jadi agar mudah diingat,  
sin-cos-tan = demi-sami-di-desa


Rumus cosec, sec, dan cotan
cosec = kebalikan sinus = 1/sin = miring / depan
sec = kebalikan cos = 1/cos = miring / samping
cotan = kebalikan tan = 1/tan = samping / depan

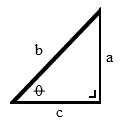
Dari gambar di atas, maka nilai trigonometri untuk sudut θ adalah :
sin θ = a/b → cosec θ = b/a
cos θ = c/b → sec θ = b/c
tan θ = a/c → cotan θ = c/a


Trigonometri Segitiga Sembarang 
Rumus-rumus di atas hanya dapat digunakan untuk segitiga yang berbentuk siku-siku. Untuk segitiga sembarang, maka tidak akan ditemukan sisi depan, samping, dan miring seperti itu. Untuk menentukan nilai trigonometri sudut-sudut pada segitiga sembarang biasanya digunakan aturan sinus dan aturan cosinus sebagai berikut :

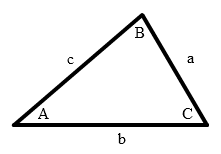
Keterangan gambar :
A = sudut A
B = sudut B
C = sudut C
a = sisi di hadapan sudut A
b = sisi di hadapan sudut B
c = sisi di hadapan sudut C

1. Aturan sinus
   Aturan sinus merupakan aturan perbandingan antara panjang sisi dengan sudut di hadapan sisi tersebut.
   
       a     =      b     =    c     
    sin A       sin B       sin C
   
   
2. Aturan cosinus
   Aturan cosinus melihat hubungan kuadrat satu sisi dengan kuadrat sisi yang lain.
   
   a² = b² + c² - 2 b.c cos A
   b² = a² + c² - 2 a.c cos B
   c² = a² + b² - 2 a.b cos C
   
   Aturan cosinus biasanya digunakan dalam menghitung resultan vektor pada bidng studi fisika. 

Identitas Trigonometri
tan θ = sin θ / cos θ
cos² θ + sin² θ = 1
1 + tan² θ  = sec² θ
1 + cotan² θ  = cosec² θ


Rumus Penjumlahan dan Pengurangan Trigonometri
sin (a ± b) = sin a cos b ± cos a sin b
sin (a + a) = sin 2a = 2 sin a. cos a
sina + sin b = 2 sin ½ (a + b) . cos ½ (a - b)
sina - sin b = 2 cos ½ (a + b). sin ½ (a - b)

cos (a ± b) = cos a cos b ∓sin a sin b
cos (a + a) = cos 2a = cos² a - sin² a
cos 2a = 2 cos² a - 1
cos 2a = 1 - 2 sin² a
cos a + cos b = 2 cos ½ (a + b) . cos ½ (a - b)
cos a - cos b = -2 sin ½ (a + b) . sin ½ (a - b)
 
tan (a ± b) = (tan a ± tan b) / (1 ∓ tan a tan b)


Rumus Perkalian Trigonometri
2 cos a cos b = cos (a + b) + cos (a - b)
2 cos a sin b = sin (a + b) - sin (a - b)

2 sin a cos b = sin (a + b) + sin (a - b)
-2 sin a sin b = cos (a + b) - cos (a - b)

Share ke Facebook >>

Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.