SUSUNAN SERI DAN PARALEL PEGAS DAN KONSTANTA PENGGANTI

Ketika sebuah pegas diberi beban pada salah satu ujungnya dan ujung yang lain dalam keadaan terikat, sehingga ia mengalami gaya tarik sebesar gaya berat beban, maka pegas akan mengalami pertambahan panajng.  Pertambahan panjang yang dialami oleh sebuah pegas dalam kondisi seperti itu berbanding lurus dengan besar gaya berat beban yang diberikan pada salah satu ujungnya. Berdasarkan hukum Hooke, jika gaya tarik tidak melampaui batas elastisitas pegas, maka perubahan panjang pegas sebanding dengan gaya pegas pemulih. Secara matematis dapat ditulis sebagai berikut :

Hukum Hooke

F = - k Δx = - k ΔL

dengan :
F = gaya pegas pemulih
k = konstanta pegas
Δx = ΔL = pertambahan panjang pegas
Tanda negatif untuk menunjukkan bahwa arah gaya pemulih selalu berlawanan dengan arah gerak pegas.

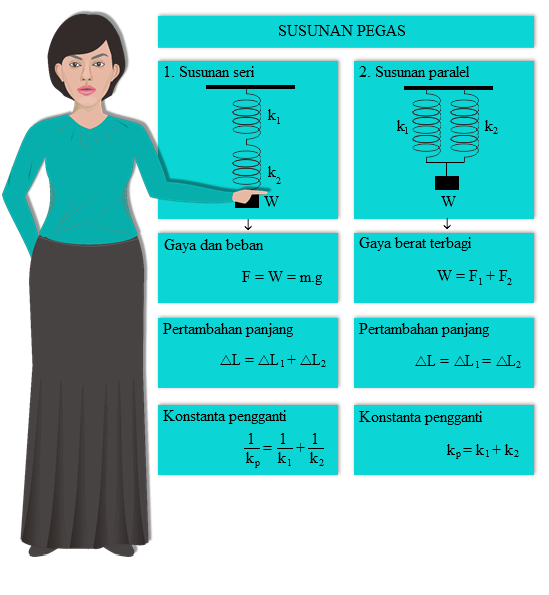
Susunan Seri Pegas

Ketika dua buah (atau beberapa) pegas disusun secara seri, maka akan berlaku beberapa sifat sebagai berikut :

1. Gaya yang bekerja pada pegas-pegas tersebut adalah sama yaitu sebesar gaya berat beban.
   F1 = F2 = W = m.g
2. Pertambahan panjang total adalah jumlah pertambahan panjang yang dialami oleh masing-masing pegas.
   ΔL = ΔL1+ ΔL2.

Dari kedua sifat di atas, maka konstanta pegas pengganti pada susunan seri adalah sebagai berikut :

Dari F = k ΔL → ΔL = F/k

⇒ ΔL = ΔL1 + ΔL2

⇒ F/kp = F1/ k1 + F2/k2

Karena F = F1 = F2 = W, maka persamaan di atas menjadi :

⇒ W/kp = W/k1 + W/k2

⇒ W/kp = (1/ k1 + 1/k2) W

⇒ 1/kp = 1/ k1 + 1/k2.

Susunan Paralel Pegas

Ketika dua buah pegas disusun secara paralel, maka akan berlaku beberapa sifat sebagai berikut :

1. Gaya yang bekerja pada pegas-pegas tersebut adalah jumlah gaya yang berkerja pada masing-masing pegas.
   
   F = W = F1 + F2
2. Pertambahan panjang total pada susunan paralel adalah sama dengan pertambahan panjang yang dialami oleh masing-masing pegas. 
   ΔL = ΔL1 = ΔL2.

Dari kedua sifat di atas, maka konstanta pegas pengganti pada susunan paralel adalah sebagai berikut :

Dari F = k ΔL
⇒ F = F1 + F2
⇒ kp ΔL =  k1 ΔL1 +  k2 ΔL2
Karena ΔL = ΔL1 = ΔL2 , maka persamaan di atas menjadi :
⇒ kp ΔL =  k1 ΔL +  k2 ΔL
⇒ kp ΔL = ( k1 + k2) ΔL
⇒ kp = k1 + k2.

Share ke Facebook >>

Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.