Jika anda berada di kelas X, maka trigonometri merupakan salah satu topik dalam bidang studi matematika yang akan anda hadapi. Trigonometri termasuk pelajaran yang tidak disukai oleh banyak murid. Akan tetapi, suka tidak suka trigonometri merupakan topik yang sangat penting karena akan digunakan dalam topik lainnya seperti lingkaran, segitiga, matriks, bahkan digunakan dalam disiplin ilmu selain matematika misalnya vektor pada bidang studi fisika dan lain sebagainya. Sebenarnya trigonometri tidak terlalu sulit jika kita dapat memahami konsep dan prinsip dasarnya. Salah satu prinsip trigonometri yang harus kita pahami adalah perbandingan trigonometri sudut-sudut istimewa. Pahamilah bahwa sudut-sudut tersebut disebut istimewa karena nilai perbandingan trigonometrinya memiliki pola tertentu yang mudah dipahami.
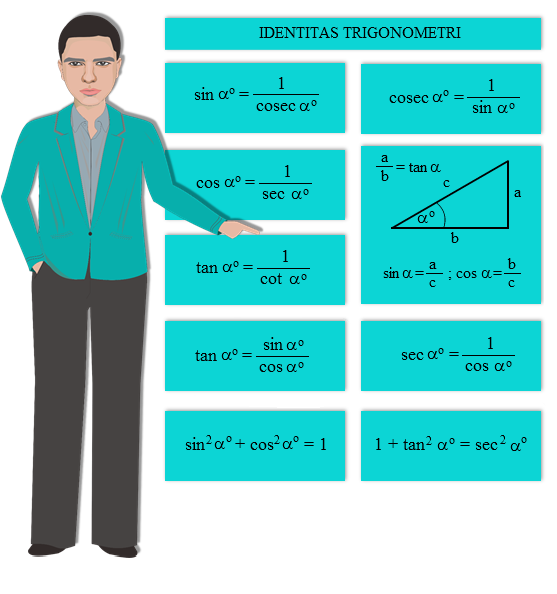
Sekedar mengingat kembali, berikut beberapa identitas trigonometri yang wajib kita hafal dan pahami. Sebelum lanjut ke tahap berikutnya, pahamilah terlebih dahulu identitas tersebut.
Sebelum membahas nilai perbandingan trigonometri sudut-sudut istimewa, ada baiknya kita membahas mengenai tanda untuk nilai perbandingan trigonometri berdasarkan kuadrannya. Tips menghapal pada bagian ini cukup sederhana. Ingat kata berikut "ASTC" yang merupakan singkatan dari "All, Sinus, Tangen, dan Cosinus". Yang harus diingat adalah bahwa singkatan tersebut masing-masing mewakili perbandingan trigonometri yang lain pada masing-masing kuadran sebagai berikut :
- Kuadran I (A)Sudut = 0o - 90o
All = semua bernilai positif. - Kuadran II (S)Sudut = 90o < θ ≤ 180o
Sin = hanya sinus dan cosecan yang positif. - Kuadran III (T)Sudut = 180o < θ ≤ 270o
Tan = hanya tangen dan cotangen yang positif. - Kuadran IV (C)Sudut = 270o < θ ≤ 360o
Cos = hanya cosinus dan secan yang positif.
Pada gambar tentang identitas trigonometri jelas terlihat hubungan sinus dengan cosecan, cosinus dengan secan, dan tangen dengan cotangen. Karena mereka merupakan hubungan kebalikan, maka agar tidak rumit, kita bisa menghafal nilai sinus, cosinus, dan tangen saja. Nilai cosec, sec, dan cot dapat kita turunkan dari sin, cosi, dan tan.
Tabel Nilai Trigonometri Sudut Istimewa
Pada tabel di bawah ini, perhatikan bahwa nilai sinus dimulai dari 0 menjadi 1 dan kembali lagi ke 0. Sebaliknya, nilai cosinus dimulai dari 1 menjadi 0 dan kembali ke 1 begitu seterusnya. Lihat bahwa beberapa sudut memiliki nilai sinus atau cosinus yang sama tapi sebagian berbeda tanda yaitu ada yang positif dan ada yang negatif. Nah untuk menentukan positif atau negatif, maka gunakanlah konsep kuadran yang telah dijelaskan di atas.| - | 0o | 30o | 45o | 60o | 90o | 120o | 135o | 150o | 180o |
| sin | 0 | ½ | ½√2 | ½√3 | 1 | ½√3 | ½√2 | ½ | 0 |
| cos | 1 | ½√3 | ½√2 | ½ | 0 | -½ | -½√2 | -½√3 | -1 |
| tan | 0 | 1/3√3 | 1 | √3 | - | -√3 | -1 | -1/3√3 | 0 |
| - | 210o | 225o | 240o | 270o | 300o | 315o | 330o | 360o |
| sin | -½ | -½√2 | -½√3 | -1 | -½√3 | -½√2 | -½ | 0 |
| cos | -½√3 | -½√2 | -½ | 0 | ½ | ½√2 | ½√3 | 1 |
| tan | 1/3√3 | 1 | √3 | - | -√3 | -1 | -1/3√3 | 0 |
Nah, di atas adalah tabel nilai perbandingan trigonometri sudut istimewa. Karena jumlahnya tidak sedikit, maka sebenarnya kita cukup menghafal sudut 0o - 90o saja. Selebihnya, kita dapat mengikuti pola tabel di atas. Untuk lebih jelasnya perhatikan contoh berikut :
Anggaplah anda sudah hafal nilai trigonometri untuk sudut 0o - 90o. Lalu anda diminta untuk menentukan nilai sin 150o, dan cos 135o. Sebenarnya ada dua trik untuk menjawab soal ini yaitu :
Anggaplah anda sudah hafal nilai trigonometri untuk sudut 0o - 90o. Lalu anda diminta untuk menentukan nilai sin 150o, dan cos 135o. Sebenarnya ada dua trik untuk menjawab soal ini yaitu :
- Anda harus hafal sudut-sudut apa saja yang istimewa dan bagaimana polanya. Perhatikan tabel di atas! Anggaplah mereka sebagai suatu barisan dengan pola yaitu diawali dari 0 kemudian ditambah 30, ditambah 15, dan ditambah 30 lagi sampai sudut 90o. Untuk sudut selanjutnya, pola tersebut berulang sampai ke sudut 360o. Nah, pada soal kita diminta untuk menentukan nilai sin 150o, dan cos 135o. Jika anda sudah hafal sudut-sudut istimewa, maka anda akan tahu bahwa sudut 150o berada di sebelah sudut 135o. Anda dapat membuat coretan kecil jika belum terlalu hafal. Tulis barisan sudut istimewa sebagai berikut :
0o 30o 45o 60o 90o 120o 135o 150o
Selanjutnya, anda harus hafal pola nilai trigonometri seperti yang terlihat pada tabel yaitu :
⇒ Untuk sinus = 0 − ½ − ½√2 − ½√3 − 1 − ½√3 − ½√2 − ½ − 0.
⇒ Untuk cosinus = 1 − ½√3 − ½√2 − ½ − 0 − ½ − ½√2 − ½√3 − 1.
- 0o 30o 45o 60o 90o 120o 135o 150o sin 0 ½ ½√2 ½√3 1 ½√3 ½√2 ½ cos 1 ½√3 ½√2 ½ 0 -½ -½√2 -½√3
Nah, berdasarkan tabel yang sudah kita buat, maka jelas terlihat bahwa :
sin 150o = ½
cos 135o = -½√2
Tahap awal memang terkesan masih rumit, tapi percayalah jika anda sudah terbiasa dengan pola itu maka anda akan langsung tahu nilainya tanpa harus membuat coretan terlebih dahulu.
- Anda harus faham konsep relasi sudut antar kuadranPada artikel sebelumnya telah dibahas rumus pebandingan trigonometri untuk sudut-sudut berelasi. Hanya ada beberapa aturan yang harus diingat yaitu :
⇒ Untuk sudut (90 ± a) dan (270 ± a) berlaku : sin = cos, cos = sin, tan = cot, cot = tan, sec = cosec, cosec = sec ; dengan tanda positif dan negatif disesuaikan berdasarkan ASTC.
⇒ Untuk sudut (180 ± a) dan (360 ± a) berlaku : sin = sin, cos = cos, tan = tan, cot = cot, sec = sec, cosec = cosec ; dengan tanda positif dan negatif disesuaikan berdasarkan ASTC.
Sekarang kembali ke soal.
sin 150o = sin (90 + 60)
⇒ sin 150o = cos 60
⇒ sin 150o = ½
Keterangan : sudut 150o berada pada kuadran II (hanya sinus dan cosecan yang positif), jadi sin 150o bernilai positif. Tanda sin berubah jadi cos karena kita menggunakan operator (90 + a).
cos 135o = cos (180 - 45)
⇒ cos 135o = - cos 45
⇒ cos 135o = -½√2.Keterangan : sudut 135o berada pada kuadran II (hanya sinus dan cosecan yang positif), jadi cos 135o bernilai negatif. Tanda cos tetap jadi cos karena kita menggunakan operator (180 - a).
Kalau kita menggunakan rumus (90 + a) untuk soal no 2, maka :
cos 135o = cos (90 + 45)
⇒ cos 135o = - sin 45
⇒ cos 135o = -½√2.
Keterangan : sudut 135o berada pada kuadran II (hanya sinus dan cosecan yang positif), jadi cos 135o bernilai negatif. Tanda cos berubah jadi sin karena kita menggunakan operator (90 + a).
Demikianlah Tips dan trik menghafal nilai trigonometri sudut istimewa. Anda merasa artikel ini bermanfaat? Jika ya, bagikanlah kepada teman-teman anda di media sosial. Terimakasih.
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.