Many students do not like trigonometry. However, like or not, trigonometry is a very important topic because it will be used in other topics such as circles, triangles, matrix, even used in other disciplines like vectors in Physics and so forth. Actually, Trigonometry is not too difficult if we can understand the concepts and basic principles of it. One of the principles that we must understand is trigonometric ratios and trigonometric values of special angles. Think this, they are called special because their trigonometric values have a certain pattern that is easily understood.
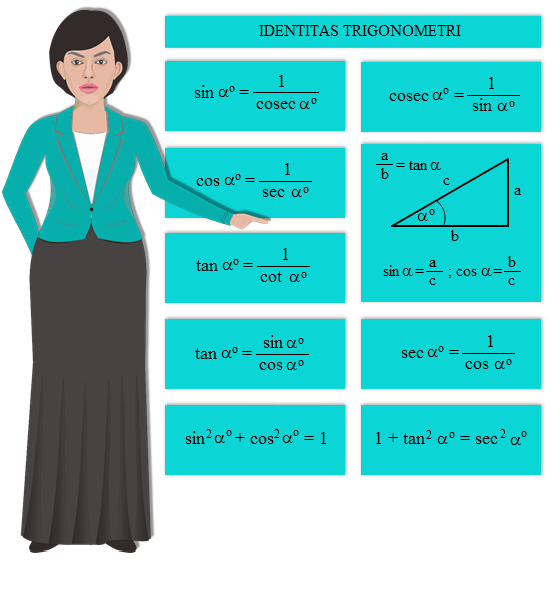
Just to recall, here some trigonometric identities that we must remember and understand. To proceed to the next step, it will be better if we understand them beforehand.
As we discussed before, we should learn about the marks (+ or -) for trigonometric
values based on their quadrant. Again, just remember this abbreviation "ASTC"
which stands for "All, Sine, Tangent, and Cosine". These abbreviations
represent each other trigonometric values in each quadrant as follows:
- First quadrant (A)⇒ Angles = 0o - 90o
⇒ All = all values are positive. - Second quadrant (S)⇒ Angles = 90o < θ ≤ 180o
⇒ Sin = the positive values only for sine and cosecant. - Third Quadrant (T)⇒ Angles = 180o < θ ≤ 270o
⇒ Tan = the positive values only for tangent and cotangent. - Fourth quadrant (C)⇒ Angles = 270o < θ ≤ 360o
⇒ Cos = the positive values only for cosine and secant.
From the picture above, we can clearly see the relationship between sine and cosecant, cosine and secant, tangent and cotangent. Since they are in reverse relationship, then we just need to memorize the values of sine, cosine, and tangent. The values of cosecant, secant, and cotangent can be calculated by their related trigonometry. For example, we can calculate the values of csc 45o by using the values of sin 45o.
Table for Trigonomeric Values of Special Angles
From the table below, we can see that the value of sines are started from 0 to 1 to 0 to 1 to 0. And the opposite, the values of cosine are started from 1 to 0 to 1 to 0 to 1. The pattern must be 0−½−½√2−½√3−1−½√3−½√2−½−0.| - | 0o | 30o | 45o | 60o | 90o | 120o | 135o | 150o | 180o |
| sin | 0 | ½ | ½√2 | ½√3 | 1 | ½√3 | ½√2 | ½ | 0 |
| cos | 1 | ½√3 | ½√2 | ½ | 0 | -½ | -½√2 | -½√3 | -1 |
| tan | 0 | 1/3√3 | 1 | √3 | - | -√3 | -1 | -1/3√3 | 0 |
| - | 210o | 225o | 240o | 270o | 300o | 315o | 330o | 360o |
| sin | -½ | -½√2 | -½√3 | -1 | -½√3 | -½√2 | -½ | 0 |
| cos | -½√3 | -½√2 | -½ | 0 | ½ | ½√2 | ½√3 | 1 |
| tan | 1/3√3 | 1 | √3 | - | -√3 | -1 | -1/3√3 | 0 |
To help us, we just need to memorize the tirgonometric values for the angles of (0o - 90o). For the other angles, we can use the pattern or use trigonometric identities. For more detail, see the following example :
We suppose that you have memorized the trigonometric values for the angles of (0o - 90o). Then you're asked for calculate sin 150o and cos 135o. For answer this question, there are two methode :
- You must remember the table above and the pattern.If you dont not completely memorize the values, you can create auxiliary table like the tabel below.
0o 30o 45o 60o 90o 120o 135o 150o
Next, you should memorize the pattern of trigonometric values.
⇒ For sine = 0 − ½ − ½√2 − ½√3 − 1 − ½√3 − ½√2 − ½ − 0.
⇒ For cosine = 1 − ½√3 − ½√2 − ½ − 0 − ½ − ½√2 − ½√3 − 1.
- 0o 30o 45o 60o 90o 120o 135o 150o sin 0 ½ ½√2 ½√3 1 ½√3 ½√2 ½ cos 1 ½√3 ½√2 ½ 0 -½ -½√2 -½√3
Well, according to the table we made, we can see that :
sin 150o = ½
cos 135o = -½√2
The first try may seem still complicated, but trust me if you are already familiar with the pattern then you will immediately know the value without having to make the auxiliary table.
- You should understand the concept of related angles. ⇒ For angles of (90 ± a) and (270 ± a) remember this :
sin = cos, cos = sin, tan = cot, cot = tan, sec = cosec, cosec = sec ;
The mark (positive and negative) is adjusted according ASTC.
⇒ For ngles of (180 ± a) and (360 ± a) remember this :
sin = sin, cos = cos, tan = tan, cot = cot, sec = sec, cosec = cosec ;
The mark (positive and negative) is adjusted according ASTC.
Now, back to the problem.
sin 150o = sin (90 + 60)
⇒ sin 150o = cos 60
⇒ sin 150o = ½
Note :
The angle of 150o is in second quadrant (sine and cosecant are positive), then sin 150o has positive value.
"sin" changes into "cos" because we use the formula for angles of (90 + a).
cos 135o = cos (180 - 45)
⇒ cos 135o = - cos 45
⇒ cos 135o = -½√2.
Note :
The angle of 135o is in second quadrant (sine and cosecant are positive), then cos 135o has negative value.
"cos" still be "cos" because we use the formula for angles of (180 - a).
For alternative solutions, we can use the formula for angles of (90 + a) to answer the second problem.
cos 135o = cos (90 + 45)
⇒ cos 135o = - sin 45
⇒ cos 135o = -½√2.
Note :
the angle of 135o is in second quadrant (sine and cosecant are positive), then cos 135o has negative value. "cos" changes into "sin" because we use the formula for angles of (90 + a).
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.

0 comments :
Post a Comment