Edutafsi.com - Sistem Katrol. Salah satu sistem yang dapat kita kaji dengan hukum Newton adalah sistem katrol. Jika sistem katrol bergerak, maka berlaku hukum kedua Newton. Jika sistem setimbang, maka berlaku hukum I Newton. Pada sistem katrol, yang perlu kita perhatikan adalah massa katrol dan gaya gesekan. Jika massa katrol dan gaya gesek diabaikan, maka besar tegangan tali pada sistem tersebut sama besar. Sebaliknya, jika massa katrol diketahui dan tidak diabaikan, maka besar tegangan talinya tidak sama. Berikut beberapa sistem katrol yang umum dipelajari.
Sedangkan gambar sebelah kanan, tegangan talinya berbeda karena massa katrol tidak diabaikan.
Karena dua sistem tersebut berbeda rumus perhitungannya, maka kita akan bahas satu persatu sebagai berikut :
#1 Massa katrol diabaikan
Ingat bahwa tegangan tali yang dialami benda 1 sama dengan tegangan tali yang dialami benda 2 (T1 = T2 = T). Pada gambar terlihat bahwa massa benda kedua lebih besar sehingga sistem bergerak ke kanan.
Tinjau benda I :
∑F = m.a
⇒ T1 - W1 = m1.a
⇒ T1 = m1.a + W1
⇒ T = m1.a + W1
Tinjau benda II :
∑F = m.a
⇒ W2 - T2 = m2.a
⇒ T2 = W2 - m2.a
⇒ T = W2 - m2.a
Karena tegangan tali sama besar, maka :
m1.a + W1 = W2 - m2.a
⇒ m1.a+ m2.a = W2 - W1
⇒ (m1 + m2) a = W2 - W1
⇒ a = (W2 - W1)/(m1 + m2)
Dengan :
a = percepatan sistem (m/s2)
W2 = berat benda kedua (N)
W1 = berat benda pertama (N)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg)
#2 Massa katrol tidak diabaikan
Jika massa katrol tidak diabaikan, maka tegangan tali kedua tidak sama dengan tegangan tali pertama (T1 ≠ T2). Selain itu, kita juga harus meninjau momen gaya yang dialami katrol.
Tinjau benda I :
∑F = m.a
⇒ T1 - W1 = m1.a
⇒ T1 = m1.a + W1
Tinjau benda II :
∑F = m.a
⇒ W2 - T2 = m2.a
⇒ T2 = W2 - m2.a
Tinjau Katrol :
∑τ = I.α
⇒ T2.r - T1.r = k mk r2 . a⁄r
⇒ (T2 - T1) r = k.mk.r.a
⇒ T2 - T1 = k.mk.a
Substitusi nilai T1 dan T2 ke persamaan ketiga :
W2 - m2.a - m1.a - W1 = k.mk.a
⇒ W2 - W1 = k.mk.a + m2.a + m1.a
⇒ W2 - W1 = (k.mk + m2 + m1) a
⇒ a = (W2 - W1) / (k.mk + m2 + m1)
Dengan :
a = percepatan sistem (m/s2)
W2 = berat benda kedua (N)
W1 = berat benda pertama (N)
k = bilangan atau konstanta pada rumus inersia katrol.
mk = massa katrol (kg)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg).
#1 Massa katrol diabaikan dan bidang licin
#2 Massa katrol dirpehitungkan dan bidang licin
Tinjau benda I :
∑F = m.a
⇒ T1 = m1.a
Tinjau benda II :
∑F = m.a
⇒ W2 - T2 = m2.a
⇒ T2 = W2 - m2.a
Tinjau Katrol :
∑τ = I.α
⇒ T2.r - T1.r = k mk r2 . a⁄r
⇒ (T2 - T1) r = k.mk.r.a
⇒ T2 - T1 = k.mk.a
Substitusi nilai T1 dan T2 ke persamaan ketiga :
W2 - m2.a - m1.a = k.mk.a
⇒ W2 = k.mk.a + m2.a + m1.a
⇒ W2 = (k.mk + m2 + m1) a
⇒ a = (W2) / (k.mk + m2 + m1)
Dengan :
a = percepatan sistem (m/s2)
W2 = berat benda kedua (N)
k = bilangan atau konstanta pada rumus inersia katrol.
mk = massa katrol (kg)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg)
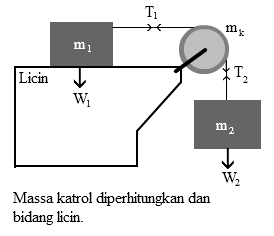
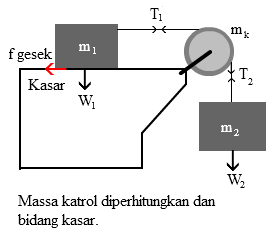
#3 Massa katrol diperhitungkan dan bidang kasar
Tinjau benda I :
∑F = m.a
⇒ T1 - Fg = m1.a
⇒ T1 = m1.a + Fg
Tinjau benda II :
∑F = m.a
⇒ W2 - T2 = m2.a
⇒ T2 = W2 - m2.a
Tinjau Katrol :
∑τ = I.α
⇒ T2.r - T1.r = k mk r2 . a⁄r
⇒ (T2 - T1) r = k.mk.r.a
⇒ T2 - T1 = k.mk.a
Substitusi nilai T1 dan T2 ke persamaan ketiga :
W2 - m2.a - m1.a - Fg = k.mk.a
⇒ W2 - Fg = k.mk.a + m2.a + m1.a
⇒ W2 - Fg = (k.mk + m2 + m1) a
⇒ a = (W2 - Fg) / (k.mk + m2 + m1)
Dengan :
a = percepatan sistem (m/s2)
W2 = berat benda kedua (N)
Fg = gaya gesek antara benda 1 dan bidang kasar (N)
k = bilangan atau konstanta pada rumus inersia katrol.
mk = massa katrol (kg)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg).
A. Sistem Katrol Sederhana
Untuk menganalisis sistem katrol sederhana seperti gambar di bawah, maka kita perlu menggambarkan garis gaya yang bekerja pada masing-masing benda. Pada gambar sebelah kiri, massa katrol diabaikan sehingga tegangan tali sama besar.Sedangkan gambar sebelah kanan, tegangan talinya berbeda karena massa katrol tidak diabaikan.
Karena dua sistem tersebut berbeda rumus perhitungannya, maka kita akan bahas satu persatu sebagai berikut :
#1 Massa katrol diabaikan
Ingat bahwa tegangan tali yang dialami benda 1 sama dengan tegangan tali yang dialami benda 2 (T1 = T2 = T). Pada gambar terlihat bahwa massa benda kedua lebih besar sehingga sistem bergerak ke kanan.
Tinjau benda I :
∑F = m.a
⇒ T1 - W1 = m1.a
⇒ T1 = m1.a + W1
⇒ T = m1.a + W1
Tinjau benda II :
∑F = m.a
⇒ W2 - T2 = m2.a
⇒ T2 = W2 - m2.a
⇒ T = W2 - m2.a
Karena tegangan tali sama besar, maka :
m1.a + W1 = W2 - m2.a
⇒ m1.a
⇒ (m1 + m2) a = W2 - W1
⇒ a = (W2 - W1)/(m1 + m2)
|
Dengan :
a = percepatan sistem (m/s2)
W2 = berat benda kedua (N)
W1 = berat benda pertama (N)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg)
Jika massa katrol tidak diabaikan, maka tegangan tali kedua tidak sama dengan tegangan tali pertama (T1 ≠ T2). Selain itu, kita juga harus meninjau momen gaya yang dialami katrol.
Tinjau benda I :
∑F = m.a
⇒ T1 - W1 = m1.a
⇒ T1 = m1.a + W1
Tinjau benda II :
∑F = m.a
⇒ W2 - T2 = m2.a
⇒ T2 = W2 - m2.a
Tinjau Katrol :
∑τ = I.α
⇒ T2.r - T1.r = k mk r2 . a⁄r
⇒ (T2 - T1) r = k.mk.r.a
⇒ T2 - T1 = k.mk.a
Substitusi nilai T1 dan T2 ke persamaan ketiga :
W2 - m2.a - m1.a - W1 = k.mk.a
⇒ W2 - W1 = k.mk.a + m2.a + m1.a
⇒ W2 - W1 = (k.mk + m2 + m1) a
⇒ a = (W2 - W1) / (k.mk + m2 + m1)
|
Dengan :
a = percepatan sistem (m/s2)
W2 = berat benda kedua (N)
W1 = berat benda pertama (N)
k = bilangan atau konstanta pada rumus inersia katrol.
mk = massa katrol (kg)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg).
B. Sistem Katrol Bidang Datar
Jika dua benda dihubungkan oleh tali dan sistem katrol, dengan salah satu benda tergantung dan benda lainnya berada di bidang datar, maka terdapat beberapa keadaan yang dapat kita amati, yaitu :#1 Massa katrol diabaikan dan bidang licin
Tinjau benda I :
∑F = m.a
⇒ T1 = m1.a
⇒ T = m1.a
Tinjau benda II :
∑F = m.a
⇒ W2 - T2 = m2.a
⇒ T2 = W2 - m2.a
⇒ T = W2 - m2.a
Karena tegangan tali sama besar, maka :
m1.a = W2 - m2.a
⇒ m1.a + m2.a = W2
⇒ (m1 + m2) a = W2
⇒ a = (W2)/(m1 + m2)
Dengan :
a = percepatan sistem (m/s2)
W2 = berat benda kedua (N)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg)
∑F = m.a
⇒ T1 = m1.a
⇒ T = m1.a
Tinjau benda II :
∑F = m.a
⇒ W2 - T2 = m2.a
⇒ T2 = W2 - m2.a
⇒ T = W2 - m2.a
Karena tegangan tali sama besar, maka :
m1.a = W2 - m2.a
⇒ m1.a + m2.a = W2
⇒ (m1 + m2) a = W2
⇒ a = (W2)/(m1 + m2)
|
Dengan :
a = percepatan sistem (m/s2)
W2 = berat benda kedua (N)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg)
Tinjau benda I :
∑F = m.a
⇒ T1 = m1.a
Tinjau benda II :
∑F = m.a
⇒ W2 - T2 = m2.a
⇒ T2 = W2 - m2.a
Tinjau Katrol :
∑τ = I.α
⇒ T2.r - T1.r = k mk r2 . a⁄r
⇒ (T2 - T1) r = k.mk.r.a
⇒ T2 - T1 = k.mk.a
Substitusi nilai T1 dan T2 ke persamaan ketiga :
W2 - m2.a - m1.a = k.mk.a
⇒ W2 = k.mk.a + m2.a + m1.a
⇒ W2 = (k.mk + m2 + m1) a
⇒ a = (W2) / (k.mk + m2 + m1)
|
Dengan :
a = percepatan sistem (m/s2)
W2 = berat benda kedua (N)
k = bilangan atau konstanta pada rumus inersia katrol.
mk = massa katrol (kg)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg)
Tinjau benda I :
∑F = m.a
⇒ T1 - Fg = m1.a
⇒ T1 = m1.a + Fg
Tinjau benda II :
∑F = m.a
⇒ W2 - T2 = m2.a
⇒ T2 = W2 - m2.a
Tinjau Katrol :
∑τ = I.α
⇒ T2.r - T1.r = k mk r2 . a⁄r
⇒ (T2 - T1) r = k.mk.r.a
⇒ T2 - T1 = k.mk.a
Substitusi nilai T1 dan T2 ke persamaan ketiga :
W2 - m2.a - m1.a - Fg = k.mk.a
⇒ W2 - Fg = k.mk.a + m2.a + m1.a
⇒ W2 - Fg = (k.mk + m2 + m1) a
⇒ a = (W2 - Fg) / (k.mk + m2 + m1)
|
Dengan :
a = percepatan sistem (m/s2)
W2 = berat benda kedua (N)
Fg = gaya gesek antara benda 1 dan bidang kasar (N)
k = bilangan atau konstanta pada rumus inersia katrol.
mk = massa katrol (kg)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg).
SUBTOPIK
- Sistem Katrol di Bidang Miring
-
Sistem Dua Katrol dan Bidang Datar
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.




Laman ini bagus sekali. Penuturannya mudah di pahami.
ReplyDeleteThanks So Ju.
Delete