Gerak melingkar berubah beraturan (GMBB) merupakan gerak melingkar yang mengalami percepatan sudut (α) konstan sehingga kecepatan sudutnya berubah teratur. Related :
- Gerak Melingkar Beraturan
- Gaya Sentripetal-Sentrifugal
- Gerak Melingkar Vertikal
- Momentun Anguler
- Kesetimbangan Rotasi
Gerak melingkar berubah beraturan ditandai dengan adanya perubahan kecepatan sudut dari waktu ke waktu. Perubahan tersebut disebabkan oleh percepatan ataupun perlambatan.
Dengan begitu dapat kita simpulkan ciri-ciri agar suatu benda dikatakan bergerak melingkar beraturan, yaitu :
Dengan begitu dapat kita simpulkan ciri-ciri agar suatu benda dikatakan bergerak melingkar beraturan, yaitu :
- Kecepatan sudut (ω) berubah teratur
- Percepatan sudut (α) konstan.
Rumus-rumus yang digunakan dalam GMBB tidak jauh berbeda dengan rumus-rumus dalam GLBB. Jika anda sudah menguasai rumus GLBB, maka rumus GMBB pasti dapat dengan mudah anda pahami. Untuk itu, berikut ini disajikan tabel perbandingan rumus GLBB dan GMBB.
Keterangan :
(+) → benda mengalami percepatan
(−) → benda mengalami perlambatan.
Dengan :
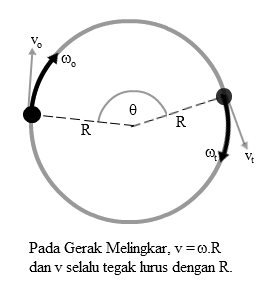
ωt = kecepatan sudut setelah t detik (rad/s)
ωo = kecepatan sudut awal (rad/s)
α = percepatan sudut (rad/s2)
θ = sudut tempuh (radian)
t = waktu yang dibutuhkan (s)
R = jari-jari lintasan (m)
Kecepatan sudut juga sering dinyatakn dalam satuan ppm (putaran per menit) ataupun rpm (rotasi per menit). Satuan tersebut menyatakan banyakanya putaran yang dilakukan benda dalam satu menit. Hubungan satuan tersebut dengan rad/s adalah :
| GLBB | GMBB | Hubungan |
|---|---|---|
| vt = vo ± a.t | ωt = ωo ± α.t | v = ω.R |
| vt2 = vo2 ± 2.a.s | ωt2 = ωo2 ± 2.α.θ | a = α. R |
| s = vo.t ± ½.a.t2 | θ = ωo.t ± ½.α.t2 | s = θ.R |
Keterangan :
(+) → benda mengalami percepatan
(−) → benda mengalami perlambatan.
Dengan :
ωt = kecepatan sudut setelah t detik (rad/s)
ωo = kecepatan sudut awal (rad/s)
α = percepatan sudut (rad/s2)
θ = sudut tempuh (radian)
t = waktu yang dibutuhkan (s)
R = jari-jari lintasan (m)
Kecepatan sudut juga sering dinyatakn dalam satuan ppm (putaran per menit) ataupun rpm (rotasi per menit). Satuan tersebut menyatakan banyakanya putaran yang dilakukan benda dalam satu menit. Hubungan satuan tersebut dengan rad/s adalah :
1 ppm = 1 rpm = π⁄30 rad/s
Contoh Soal :
- Sebuah benda berotasi dengan kecepatan 120⁄π ppm. Jika setelah 10 detik benda tersebut berhenti, maka hitunglah besar sudut yang ditempuh benda tersebut.
Pembahasan :
Dik : ωo = 120⁄π ppm = 120⁄π (π⁄30) = 4 rad/s; t = 10 s; ωt = 0.
Karena ωt < ωo, maka benda diperlambat.
ωt = ωo − α.t
⇒ 0 = 4 − 10α
⇒ 10α = 4
⇒ α = 4⁄10
⇒ α = 0,4 rad/s2
Maka sudut tempuhnya adalah :
ωt2 = ωo2 − 2.α.θ
⇒ (0)2 = (4)2 − 2.(0,4).θ
⇒ 0 = 16 - 0,8 θ
⇒ 0,8 θ = 16
⇒ θ = 16⁄0,8
⇒ θ = 20 radian. - Sebuah partikel berotasi dengan kecepatan sudut awal 20 rad/s. Jika pada detik ke-8 kecepatan sudut partikel menjadi 10 rad/s, tentukan pada detik ke berapa partikel akan berhenti.
Pembahasan :
Dik : ωo = 20 rad/s; t = 8 s; ωt = 10 rad/s.
Karena ωt < ωo, maka benda diperlambat.
ωt = ωo − α.t
⇒ 10 = 20 − 8α
⇒ 8α = 20 − 10
⇒ 8α = 10
⇒ α = 10⁄8
⇒ α = 5⁄4 rad/s2
Saat berhenti berarti ωt = 0.
ωt = ωo − α.t
⇒ 0 = 20 − (5⁄4) t
⇒ 5⁄4 t = 20
⇒ t = 16 s.
- Sebuah benda berupa silinder pejal dengan massa 4 kg berjari-jari 1 m berotasi dari keadaan diam akibat momen gaya sebesar 8 Nm. Berapakah kecepatan sudut benda setelah 10 detik.
Pembahasan :
Dik : m = 4 kg; R = 1 m; ωo = 0; τ = 8 Nm; t = 10 s.
Karena untuk menentukan kecepatan sudut pada detik tertentu harus diketahui percepatannya, maka kita harus mencari nilai percepatannya terlebih dahulu. Dari τ = I α, kita peroleh :
τ = I α
⇒ 8 = ½ m.r2 .α
⇒ 8 = ½ (4).(1)2 .α
⇒ 8 = 2 α
⇒ α = 4 rad/s2
Dengan begitu diperoleh :
ωt = ωo + α.t
⇒ ωt = 0 + (4) (10)
⇒ ωt = 40 rad/s.
- Sebuah benda berotasi dengan kecepatan sudut 40 rad/s. Jika setelah 2 detik kecepatan sudutnya menjadi 80 rad/s, maka hitunglah sudut tempuhnya.
Pembahasan :
Dik ωo = 40 rad/s; t = 2 s; ωt = 80 rad/s.
Karena ωt > ωo, maka benda dipercepat.
ωt = ωo + α.t
⇒ 80 = 40 + 2α
⇒ 40 = 2α
⇒ α = 20 rad/s2
Sudut yang ditempuh :
ωt2 = ωo2 + 2.α.θ
⇒ (80)2 = (40)2 + 2.(20).θ
⇒ 6400 = 1600 + 40 θ
⇒ 4800 = 40 θ
⇒ θ = 480⁄4
⇒ θ = 120 radian.
- Agar benda yang berotasi dengan kecepatan 6 rad/s menempuh sudut 80 rad dalam waktu 5 detik, tentukanlah percepatan yang dibutuhkannya.
Pembahasan :
Dik ωo = 6 rad/s; θ = 80 rad; t = 5 s.
Karena ωt tidak diketahui, maka kita gunakan rumus ketiga :
θ = ωo.t + ½.α.t2⇒ 80 = 6 (5) + ½.α.(5)2
⇒ 80 = 30 + 12,5α
⇒ 50 = 12,5α
⇒ α = 4 rad/s2.
(Corrected by Sinjiru Setyawan 3-03-16)
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.
no 5 jawaban salah. 1/2 tidak ddihitung. jawaban yang benar 4 rad/s^2
ReplyDeleteTerimakasih atas koreksinya Sinjiru Setyawan.
Delete