Kesetimbangan benda tegar termasuk materi yang sering muncul dalam soal ujian nasional bidang studi fisika. Setiap tahun setidaknya terdapat satu soal yang berhubungan dengan dinamika rotasi.
Momen Inersia Momen Gaya (Torsi)
Kesetimbangan Rotasi
Pembahasan Sistem Katrol
Pertanyaan tentang kesetimbangan benda tegar yang seringkali muncul dalam soal ujian nasional adalah besar tegangan tali agar sistem seimbang, besar gaya yang diberikan, dan berat benda yang digantung.
Berikut beberapa soal ujian nasional tentang kesetimbangan benda tegar.
UN Fisika 2006/2007
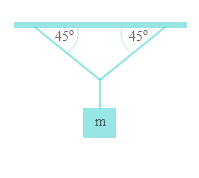
- Sistem berada dalam kesetimbangan. Jika berat beban adalah 500√2 N, besar tegangan tali yang membentuk sudut 45o adalah ....
A. Nol D. 375 N B. 150 N E. 500 N C. 250 N Pembahasan :
Untuk menjawab soal seperti ini kita dapat menggunakan konsep Aturan sinus. Untuk itu kita tentukan terlebih dahulu besar sudut yang berada di hadapan masing-masing gaya sebagai berikut :
Dari gambar jelas terlihat bahwa pada titik kesetimbangan terdapat tiga gaya yang bekerja yaitu T1, T2, dan T3. Besar tegangan tali T1 = T2 karena besar sudutnya sama. Karena besar tegangan T3 sama dengan berat beban yang digantung, maka :
T2 = T3 sin 135 sin 90 T2 = W sin 135 sin 90
⇒ T2 = 500√2 (½√2)T2 = 500√2 ½√2 1
⇒ T2 = 500 N
Jadi, T1 = T2 = 500 N (Opsi E).
- Pada tengah-tengah batang AB digantungkan sebuah balok bermassa 8 kg. Besarnya tegangan tali bila massa batang diabaikan adalah ....
Dalam keadan setimbang berlaku :
∑ τ = 0
⇒ W (½AB) − T sin 30 (AB) = 0
⇒ W (½AB) = T (½) (AB)
⇒ W(½AB)= T(½AB)
⇒ W = T
⇒ T = m.g
⇒ T = 8 (10)
⇒ T = 80 N (Opsi B).
UN Fisika 2007/2008
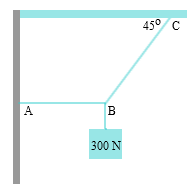
- Sistem berada dalam keadaan setimbang. Besar tegangan tali BC adalah ....
A. Nol D. 300√2 N B. 300 N E. 600√2 N C. 300√3 N
Pembahasan :
Dengan konsep aturan sinus diperoleh :
Tbc = Tb sin 90 sin 135 Tbc = W sin 90 sin 135 Tbc = 300 1 ½√2 Tbc = 600 √2
⇒ Tbc = 300√2Tbc = 600 . √2 √2 √2
Jadi, Tbc = 300√2 N (Opsi D).
- Pada sisem kesetimbangan benda tegar di bawah ini, batang AB homogen panjang 80 cm beratnya 18 N, pada ujung B digantung beban yang beratnya 30 N, batang ditahan oleh tali BC. Jika jarak AC = 60 cm, tegangan pada tali adalah ....
A. 36 N D. 65 N B. 48 N E. 80 N C. 50 N
Pembahasan :
Pada gambar segitiga ABC, diketahui AB = 80 cm, AC = 60 cm. Berdasarkan dalil Phytagoras, maka panjang BC adalah 100 cm. Dengan begitu sin B = sin θ = 60⁄10 = 0,6. Karena massa batang tidak diabaikan maka gaya yang menghasilkan torsi ada tiga gaya yaitu berat beban (W), berat batang (Wab), dan tegangan tali (T sin θ).
Dalam keadan setimbang berlaku :
∑ τ = 0
⇒ W (AB) + Wab (½AB) − T sin θ (AB) = 0
⇒ W (AB)+ Wab (½AB) = T sin θ (AB)
⇒ 30 (80) + 18 (40) = T (0,6) (80)
⇒ 30 (80) + 9 (80) = 0,6 T (80)
⇒ (30 + 9)80= 0,6 T(80)
⇒ 39 = 0,6 T
⇒ T = 65 N (Opsi D).
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.



0 comments :
Post a Comment