Edutafsi.com - Energi Kinetik Rotasi. Ketika sebuah benda memiliki momen inersia I berotasi dengan kecepatan sudut ω, maka benda tersebut akan memiliki energi kinetik rotasi sebesar Ekr. Benda yang bergerak memiliki energi kinetik. Kita tahu, ketika sebuah benda bermassa m bergerak dengan kecepatan v, maka benda tersebut akan memiliki energi kinetik sebesar Ekt.
Ketika sebuah benda berotasi maka besar energi kinetik rotasi yang dimilikinya adalah sebanding dengan hasil kali momen inersia dan kuadrat kecepatan sudutnya. Secara matematis, besar energi kinetik rotasi dapat dihitung dengan rumus berikut :
| Ekr = ½ I.ω2 |
Dengan :
Ekr = energi kinetik rotasi (Joule)
I = momen inersia (kg.m2)
ω = kecepatan sudut (rad/s).
Energi Kinetik Benda Menggelinding
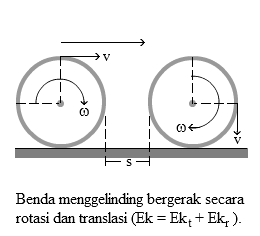
Ketika sebuah benda menggelinding, maka benda tersebut melakukan dua gerak selakigus yaitu gerak rotasi dan gerak translasi sehingga energi kinetik total benda adalah jumlah energi kinetik translasi dan energi kinetik rotasi. Secara matematis dapat ditulis :
| Ektotal = Ekt + Ekr |
| Ektotal = ½ m.v2 + ½ I.ω2 |
Dengan :
Ektotal = energi kinetik total(Joule)
Ekt = energi kinetik translasi (Joule)
Ekr = energi kinetik rotasi (Joule)
m = massa benda (kg)
v = kecepatan linear benda (m/s)
I = momen inersia (kg.m2)
ω = kecepatan sudut (rad/s)
m = massa benda (kg)
v = kecepatan linear benda (m/s)
I = momen inersia (kg.m2)
ω = kecepatan sudut (rad/s)
Persamaan di atas dapat disederhanakan dengan penurunan rumus berikut ini :
⇒ Ektotal = Ekt + Ekr
⇒ Ektotal = ½ m.v2 + ½ I.ω2
⇒ Ektotal = ½ m.v2 + ½ (k.m.R2).(v⁄R)2
⇒ Ektotal = ½ m.v2 + ½ k.m.v2
⇒ Ektotal = ½ m.v2 + k ½ m.v2
⇒ Ektotal = ½ m.v2 (1 + k)
Dengan :
k = bilangan skalar pada rumus momen inersia benda.
(misal untuk silinder pejal k = ½).
⇒ Ektotal = ½ m.v2 + k ½ m.v2
⇒ Ektotal = ½ m.v2 (1 + k)
| Ektotal = ½ m.v2 (1 + k) |
Dengan :
k = bilangan skalar pada rumus momen inersia benda.
(misal untuk silinder pejal k = ½).
Contoh 1 : Energi Kinetik Rotasi
Sebuah benda berbentuk bola pejal memiliki massa 5 kg dan jari-jari 20 cm. Jika benda berotasi dengan kecepatan sudut 40 rad/s, maka tentukanlah energi kinetik rotasi benda.
Pembahasan :
Dik : m = 5 kg; r = 0,2 m; ω = 4 rad/s.
Ingat, momen inersia bola pejal dihitung dengan rumus :
I = ⅖ m.R2
⇒ I = ⅖ (5).(0,2)2
⇒ I = ⅖ (5) (0,04)
⇒ I = 0,08 kg m2
Maka energi kinetik rotasi benda adalah :
Ekr = ½ I.ω2
⇒ Ekr = ½ (0,08).(4)2
⇒ Ekr = ½ (0,08).(16)
⇒ Ekr = 0,64 Joule.
Contoh 2 : Energi Kinetik Bola Pejal
Sebuah bola pejal bertranslasi dan berotasi dengan kecepatan linear dan kecepatan sudut masing-masing v dan ω. Tentukan energi kinetik total bola pejal tersebut dalam bentuk v.
Pembahasan :
Untuk bola pejal, I = ⅖ m.R2, maka k = ⅖.
Berdasarkan penurunan rumus yang telah dibahas di atas, maka :
Ektotal = ½ m.v2 (1 + k)
⇒ Ektotal = ½ m.v2 (1 + ⅖)
⇒ Ektotal = ½ m.v2 (7⁄5)
⇒ Ektotal = 7⁄10 m.v2
Contoh 3 : Hubungan Energi Kinetik dan Momen Inersia
Seorang penari balet berputar 60⁄π ppm dengan kedua lengannya direntangkan. Pada saat itu momen inersia penari 8 kg.m2. Kemudian kedua lengannya dirapatkan sehingga momen inersianya menjadi 2 kg.m2. Tentukanlah energi kinetik rotasi penari setelah momen inersianya berubah.
Pembahasan :
Dik ω1 = 60⁄π ppm = 60⁄π (π⁄30) = 2 rad/s.
Dengan menggunakan hukum kekealan momentum sudut, maka diperoleh kecepatan sudut penari setelah momen inresianya berubah, yaitu :
I1.ω1 = I2.ω2
⇒ 8 (2) = 2 ω2
⇒ ω2 = 8 rad/s
Maka energi kinetik rotasi benda adalah :
Ekr = ½ I.ω2
⇒ Ekr = ½ (2).(8)2
⇒ Ekr = ½ (2).(64)
⇒ Ekr = 64 Joule.
Contoh 4 : Energi Kinetik Rotasi pada Detik ke-t
Benda berupa cakram bermassa 4 kg berjari-jari 0,1 m mula-mula berotasi dengan kecepatan 4 rad/s. Jika benda dipercepat 2 rad/s2, maka tentukanlah energi kinetik rotasi benda setelah 4 detik.
Pembahasan :
Dengan rumus GMBB, kita peroleh kecepatan sudut setelah 4 detik.
ωt = ωo + α.t
⇒ ωt = 4 + (2) (4)
⇒ ωt = 12 rad/s.
Momen inersia cakram atau silinder pejal adalah :
I = ½ m.R2
⇒ I = ½ (4).(0,1)2
⇒ I = 0,02 kg m2
Energi kinetik rotasi benda adalah :
Ekr = ½ I.ω2
⇒ Ekr = ½ (0,02).(12)2
⇒ Ekr = ½ (0,02).(144)
⇒ Ekr = 1,44 Joule.
Contoh 5 : Menentukan Kecepatan Gelinding
Sebuah bola pejal bermassa 5 kg yang mula-mula diam dilepaskan dari ujung sebuah bidang miring dan mulai menggelinding. Jika ketinggian h = 2,52 m, tentukanlah kecepatan bola saat tiba di ujung bawah bidang miring.
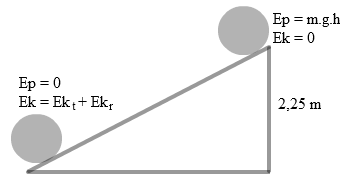
Pembahasan :
Berdasarkan Hukum Kekekalan Energi Mekanik :
Ep1 + Ek1 = Ep2 + Ek2
⇒ Ep1 + 0 = 0 + Ek2
⇒ Ep1 = Ek2
⇒ Ep1 = Ekt + Ekr
⇒ m.g.h1 = ½ m.v2 (1 + k)
⇒ m.g.h1 = ½ m.v2 (1 + ⅖)
Sebuah benda berbentuk bola pejal memiliki massa 5 kg dan jari-jari 20 cm. Jika benda berotasi dengan kecepatan sudut 40 rad/s, maka tentukanlah energi kinetik rotasi benda.
Pembahasan :
Dik : m = 5 kg; r = 0,2 m; ω = 4 rad/s.
Ingat, momen inersia bola pejal dihitung dengan rumus :
I = ⅖ m.R2
⇒ I = ⅖ (5).(0,2)2
⇒ I = ⅖ (5) (0,04)
⇒ I = 0,08 kg m2
Maka energi kinetik rotasi benda adalah :
Ekr = ½ I.ω2
⇒ Ekr = ½ (0,08).(4)2
⇒ Ekr = ½ (0,08).(16)
⇒ Ekr = 0,64 Joule.
Sebuah bola pejal bertranslasi dan berotasi dengan kecepatan linear dan kecepatan sudut masing-masing v dan ω. Tentukan energi kinetik total bola pejal tersebut dalam bentuk v.
Pembahasan :
Untuk bola pejal, I = ⅖ m.R2, maka k = ⅖.
Berdasarkan penurunan rumus yang telah dibahas di atas, maka :
Ektotal = ½ m.v2 (1 + k)
⇒ Ektotal = ½ m.v2 (1 + ⅖)
⇒ Ektotal = ½ m.v2 (7⁄5)
⇒ Ektotal = 7⁄10 m.v2
Contoh 3 : Hubungan Energi Kinetik dan Momen Inersia
Pembahasan :
Dik ω1 = 60⁄π ppm = 60⁄π (π⁄30) = 2 rad/s.
Dengan menggunakan hukum kekealan momentum sudut, maka diperoleh kecepatan sudut penari setelah momen inresianya berubah, yaitu :
I1.ω1 = I2.ω2
⇒ 8 (2) = 2 ω2
⇒ ω2 = 8 rad/s
Maka energi kinetik rotasi benda adalah :
Ekr = ½ I.ω2
⇒ Ekr = ½ (2).(8)2
⇒ Ekr = ½ (2).(64)
⇒ Ekr = 64 Joule.
Contoh 4 : Energi Kinetik Rotasi pada Detik ke-t
Pembahasan :
Dengan rumus GMBB, kita peroleh kecepatan sudut setelah 4 detik.
ωt = ωo + α.t
⇒ ωt = 4 + (2) (4)
⇒ ωt = 12 rad/s.
Momen inersia cakram atau silinder pejal adalah :
I = ½ m.R2
⇒ I = ½ (4).(0,1)2
⇒ I = 0,02 kg m2
Energi kinetik rotasi benda adalah :
Ekr = ½ I.ω2
⇒ Ekr = ½ (0,02).(12)2
⇒ Ekr = ½ (0,02).(144)
⇒ Ekr = 1,44 Joule.
Contoh 5 : Menentukan Kecepatan Gelinding

Pembahasan :
Berdasarkan Hukum Kekekalan Energi Mekanik :
Ep1 + Ek1 = Ep2 + Ek2
⇒ Ep1 + 0 = 0 + Ek2
⇒ Ep1 = Ek2
⇒ Ep1 = Ekt + Ekr
⇒ m.g.h1 = ½ m.v2 (1 + k)
⇒ m.g.h1 = ½ m.v2 (1 + ⅖)
⇒ m.g.h1 = 7⁄10 m.v2
⇒ g.h1 = 7⁄10 v2
⇒ (10) (2,52) = 7⁄10 v2
⇒ 252 = 7 v2
⇒ v2 = 252⁄7
⇒ v2 = 36
⇒ v = 6 m/s.
⇒ g.h1 = 7⁄10 v2
⇒ (10) (2,52) = 7⁄10 v2
⇒ 252 = 7 v2
⇒ v2 = 252⁄7
⇒ v2 = 36
⇒ v = 6 m/s.
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.