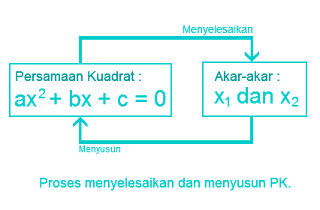
Secara umum, persamaan kuadrat dinyatakan dengan ax2 + bx + c = 0. Jika nilai dari koefisien a, b, dan c diketahui, maka pertanyaan yang umum diajukan adalah menentukan akar-akar persamaan kuadrat. Sebaliknya, jika koefisien a, b, dan c tidak diketahui, maka kita dapat menentukannya dengan menggunakan akar persamaan kuadrat jika akar-akar tersebut diketahui. Jika akar-akarnya diketahui, maka pertanyaan yang umum diajukan adalah menentukan atau menyusun persamaan kuadratnya.
Seperti yang telah dibahas sebelumnya, untuk menyusun persamaan kuadrat baru kita dapat melihat hubungan antara akar-akar persamaan kuadrat baru dengan akar-akar persamaan kuadrat yang diketahui. Menyusun persamaan kuadrat jika akar-akarnya diketahui juga tidak jauh berbeda dengan cara itu. Ada dua metode yang dapat kita gunakan untuk menyusun persamaan kuadrat jika akar-akarnya diketahui, yaitu :
Metode Faktor
Seperti yang kita tahu, kita dapat menggunakan metode pemfaktoran untuk menentukan akar-akar persamaan kuadrat. Maka, jika akar-akar suatu persamaan kuadrat diketahui, kita juga dapat menyusun persamaan kuadrat dengan memakai konsep faktor.
Jika x1 dan x2 adalah akar-akar dari suatu persamaan kuadrat, maka persamaan kuadrat tersebut dapat disusun dengan rumus berikut ini :
(x − x1)(x − x2) = 0 Contoh :
Susunlah persamaan kuadrat yang akar-akarnya diketahui sebagai berikut :
- 2 dan 4
- -1 dan 6
- -4 dan 8
- 3 dan 2
- -3 dan -4
Pembahasan :
- x1 = 2 dan x2 = 4⇒ (x − x1)(x − x2) = 0
⇒ (x − 2)(x − 4) = 0
⇒ x2 − 4x − 2x + 8 = 0
⇒ x2 − 6x + 8 = 0 - x1 = -1 dan x2 = 6⇒ (x − x1)(x − x2) = 0
⇒ (x − (-1))(x − 6) = 0
⇒ (x + 1)(x − 6) = 0
⇒ x2 − 6x + x − 6 = 0
⇒ x2 − 5x − 6 = 0 - x1 = -4 dan x2 = 8⇒ (x − x1)(x − x2) = 0
⇒ (x − (-4))(x − 8) = 0
⇒ (x + 4)(x − 8) = 0
⇒ x2 − 8x + 4x − 32 = 0
⇒ x2 − 4x − 32 = 0 - x1 = 3 dan x2 = 2⇒ (x − x1)(x − x2) = 0
⇒ (x − 3)(x − 2) = 0
⇒ x2 − 2x − 3x + 6 = 0
⇒ x2 − 5x + 6 = 0 - x1 = -3 dan x2 = -4⇒ (x − x1)(x − x2) = 0
⇒ (x − (-3))(x − (-4)) = 0
⇒ (x + 3)(x + 4) = 0
⇒ x2 + 4x + 3x + 12 = 0
⇒ x2 + 7x + 12 = 0
Memakai Rumus Jumlah dan Hasil Kali Akar
Metode yang kedua adalah menggunakan jumlah dan hasil kali akar. Seperti yang telah dibahas dalam beberapa artikel sebelumnya, rumus jumlah dan hasil kali akar adalah sebagai berikut :
x1 + x2 = -b⁄a x1 . x2 = c⁄a
Bila masing-masing ruas pada persamaan kuadrat ax2 + bx + c = 0 dibagi dengan nilai a, maka persamaannya akan menjadi :
⇒ x2 + b⁄a x + c⁄a = 0
Jika kita hubungkan dengan rumus jumlah dan hasil kali akar, maka kita dapat menyusun persamaan kuadrat dengan rumus berikut ini :
x2 − (x1 + x2)x + (x1 . x2) = 0
Contoh :
Susunlah persamaan kuadrat yang akar-akarnya diketahui sebagai berikut :
- 2 dan 4
- -1 dan 6
- -4 dan 8
- 3 dan 2
- -3 dan -4
Pembahasan :
- x1 = 2 dan x2 = 4⇒ x2 − (x1 + x2)x + (x1 . x2) = 0
⇒ x2 − (2 + 4)x + (2 x 4) = 0
⇒ x2 − 6x + 8 = 0 - x1 = -1 dan x2 = 6⇒ x2 − (x1 + x2)x + (x1 . x2) = 0
⇒ x2 − (-1 + 6)x + (-1 x 6) = 0
⇒ x2 − 5x − 6 = 0 - x1 = -4 dan x2 = 8⇒ x2 − (x1 + x2)x + (x1 . x2) = 0
⇒ x2 − (-4 + 8)x + (-4 x 8) = 0
⇒ x2 − 4x − 32 = 0 - x1 = 3 dan x2 = 2⇒ x2 − (x1 + x2)x + (x1 . x2) = 0
⇒ x2 − (3 + 2)x + (3 x 2) = 0
⇒ x2 − 5x + 6 = 0 - x1 = -3 dan x2 = -4⇒ x2 − (x1 + x2)x + (x1 . x2) = 0
⇒ x2 − (-3 + (-4))x + (-3 x (-4)) = 0
⇒ x2 + 7x + 12 = 0
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.