PERKALIAN SKALAR (DOT PRODUCT) DUA VEKTOR

Perkalian dua vektor dapat dibedakan menjadi perkalian titik (dot product) yang biasa disebut perkalian skalar, dan perkalian silang (cross product) yang biasa disebut perkalian vektor. Perkalian skalar atau perkalian titik antara dua vektor menghasilkan nilai skalar sedangkan perkalian silang antara dua vektor menghasilkan vektor pula. Perkalian titik dua vektor didefenisikan sebagai suatu sakalar yang nilainya sama dengan hasil kali antara besar kedua vektor dengan cosinus sudut apitnya.

Perkalian skalar dua vektor dapat dikaji secara geometris ataupun secara aljabar. Hasil yang diperoleh berdasarkan dua metode tersebut adalah sama besar. Berikut rumus perkalian skalar :

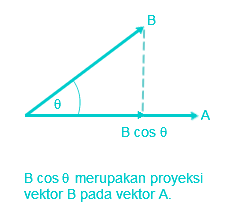
1. Perkalian Skalar Secara Geometris

   Secara geometris, perkalian skalar antara dua vektor adalah hasil kali antara besar vektor pertama dengan proyeksi vektor kedua.
   Secara matematis perkalian skalar dua vektor dapat ditentukan dengan rumus :
   
   a . b = |a|.|b| cos θ
   
   Dengan :
   |a| = besar vektor a
   |b| = besar vektor b
   θ = sudut antara vektor a dan b.
   
   Misal dua vektor A dan B dinyatakan dengan :
   A = aî + bĵ  + ck̂
   B = kî + mĵ  + nk̂
   
   Maka perkalian skalar antara A dan B adalah :
   ⇒ A.B = |A|.|B| cos θ
   ⇒ A.B = √a² + b² + c².√k² + m² + n² cos θ
   
   Rumus perkalian skalar di atas biasanya digunakan untuk menentukan besar sudut antara dua vektor dengan menggunakan hasil kali berdasarkan perhitungan aljabar. Selain itu, rumus ini juga digunakan untuk menentukan nilai variabel dalam vektor jika sudut apitnya diketahui.
   
   Contoh :
   

   1. Diketahui vektor A = 2î + 5ĵ  + 4k̂ dan B = î + 2ĵ  − 3k̂. Sudut antara A dan B adalah ....

      A. 90o	D. 45o
      B. 60o	E. 30o
      C. 53o

      
      Pembahasan :
      Berdasarkan rumus perkalian skalar :
      ⇒ A.B = |A|.|B| cos θ
      ⇒ (2î + 5ĵ  + 4k̂)(î + 2ĵ  − 3k̂) = |A|.|B| cos θ  
      ⇒ 2(1) + 5(2) + (4)(-3) = |A|.|B| cos θ  
      ⇒ 2 + 10 − 12 = |A|.|B| cos θ  
      ⇒ 0 = |A|.|B| cos θ   
      ⇒ cos θ = 0
      ⇒ θ = 90^o
      

      Jawaban : A

      
      
   2. Diketahui vektor a = 2î + 4ĵ  − nk̂ dan B = î + 2ĵ  + 2k̂. Jika kedua vektor tersebut saling tegak lurus, maka nilai n adalah .....

      A. 100 m	D. 115 m
      B. 105 m	E. 125 m
      C. 110 m

      
      Pembahasan :
      Berdasarkan konsep perkalian skalar secara geometris :
      ⇒ a.b = |a|.|b| cos θ
      ⇒ a.b = |a|.|b| cos 90^o
      ⇒ (2î + 4ĵ  − nk̂).(î + 2ĵ  + 2k̂) = |a|.|b| (0)
      ⇒ 2(1) + 4(2) + (-n)(2) = 0
      ⇒ 2 + 8 − 2n = 0
      ⇒ 10 − 2n = 0
      ⇒ -2n = -10
      ⇒ n = 5




2. Perkalian Skalar Secara Aljabar

   Misal dua vektor A dan B dinyatakan dengan :
   A = aî + bĵ  + ck̂
   B = kî + mĵ  + nk̂
   
   Maka perkalian skalar antara A dan B adalah :
   ⇒ A.B = a(k) + b(m) + c(n)
   
   Contoh :
   Vektor a dan b diberikan sebagai berikut :
   

   a =	2	dan b =	4
   	-1		2
   	-3		-1

   
   Tentukan hasil perkalian skalar antara a dan b.
   
   
   Pembahasan :
   ⇒ a.b = a(k) + b(m) + c(n)
   ⇒ a.b = (2î − ĵ − 3k̂)(4î + 2ĵ − k̂)
   ⇒ a.b = 2(4) + (-1)(2) + (-3)(-1)
   ⇒ a.b = 8 − 2 + 3
   ⇒ a.b = 9
   
   

Share ke Facebook >>

Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.