PEMBAHASAN SBMPTN MATEMATIKA PERSAMAAN DAN FUNGSI LOGARITMA

1. Jika diketahui persamaan logaritma ^xlog 2 + ^xlog (3x - 4) = 2 mempunyai dua penyelesaian yaitu x₁ dan x₂, maka hasil kali akar-akarnya adalah ....

   A. x1.x2 = 8

   B. x1.x2 = 6

   C. x1.x2 = 4

   D. x1.x2 = 3

   E. x1.x2 = 2

   
   Pembahasan :
   Sifat logaritma yang kita gunakan untuk soal ini adalah :
   

   alog b + alog c = alog(b.c)

   alog ab = b

   
   
   Dengan menggunakan sifat logaritma tersebut, maka bentuk persamaan logaritma pada soal dapat kita sederhanakan menjadi :
   ⇒ ^xlog 2 + ^xlog (3x - 4) = 2
   ⇒ ^xlog {2(3x - 4)} = 2
   ⇒ ^xlog (6x - 8) = ^xlog x²
   ⇒ 6x - 8 = x²
   ⇒ x² - 6x + 8 = 0
   
   Bentuk sederhana di atas merupakan bentuk persamaan kuadrat yang memiliki akar-akar x₁ dan x₂. Hasil kali akar-akar suatu persamaan kuadrat dapat kita tentukan dengan mencari akar-akarnya terlebih dahulu atau dengan menggunakan rumus berikut :
   

   x1 . x2 = c⁄a

   
   Dari persamaan kuadrat yang kita peroleh, diketahui :
   ⇒ x² - 6x + 8 = 0
   ⇒ a = 1; b = -6; c = 8.
   
   Dengan demikian, hasil kali akar-akarnya adalah :
   ⇒ x₁ . x₂ = ^c⁄_a
   ⇒ x₁ . x₂ = ⁸⁄₁
   ⇒ x₁ . x₂ = 8
   

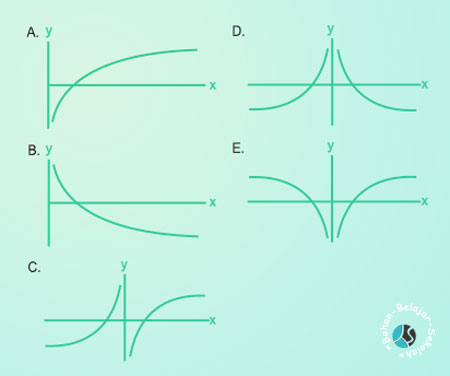
   Jawaban : A
   
   
2. Grafik fungsi y = log x² adalah ....
   
   
   

   
   
   Pembahasan :
   Berikut sifat logaritma yang dapat kita gunakan :
   

   alog b2 = 2. alog |b|

   
   
   Berdasarkan sifat di atas, fungsi soal dapat kita ubah menjadi :
   ⇒ y = log x²
   ⇒ y = 2 log |x|
   
   Karena basis logaritmanya 10, kita bisa menentukan beberapa titik bantu, yaitu :
   Untuk x = 1 dan x = -1
   ⇒ y = 2 log |x|
   ⇒ y = 2 log 1
   ⇒ y = 2 log 10⁰
   ⇒ y = 2 (0)
   ⇒ y = 0
   Titik (1, 0) dan (-1,0)
   
   Untuk x = 10 dan x = -10
   ⇒ y = 2 log |x|
   ⇒ y = 2 log 10
   ⇒ y = 2 (1)
   ⇒ y = 2
   Titik (10, 2) dan (-10,2)
   
   Dengan menghubungkan titik-titik bantu tersebut (seperti grafik eksponen), maka grafik fungsi y = log x² kurang lebih seperti gambar di bawah ini.
   

   

     Jawaban : E
   
   
3. Jika ⁸¹log ¹⁄_x = ^xlog ¹⁄_y = ^ylog ¹⁄₈₁, maka 2x - 3y sama dengan ....

   A. -162	D. 81
   B. -81	E. 162
   C. 0

   
   Pembahasan :
   Sifat logaritma yang kita gunakan :
   

   alog b . blog c . clog d = alog d

   
   Karena ketiga bentuk logaritma bernilai sama, maka misalkan nilainya sama dengan p. Selanjutnya kita gunakan sifat perkalian logaritma di atas untuk menentukan nilai p.
   ⇒  ⁸¹log ¹⁄_x . ^xlog ¹⁄_y . ^ylog ¹⁄₈₁ = p.p.p
   ⇒  ⁸¹log ¹⁄_x . ^xlog ¹⁄_y . ^ylog ¹⁄₈₁ = p³
   ⇒  ⁸¹log x^-1. ^xlog y^-1 . ^ylog (81)^-1 = p³
   ⇒ (-1)⁸¹log x . (-1)^xlog y . (-1)^ylog 81 = p³
   ⇒ (-1)³ (⁸¹log x . ^xlog y . ^ylog 81) = p³
   ⇒ (-1) ⁸¹log 81 = p³
   ⇒ -1 = p³
   ⇒ p = -1
   
   Karena pada soal ditanya nilai 2x - 3y, maka kita harus mencari nilai x dan y terlebih dahulu.
   Menentukan nilai x :
   ⇒ ⁸¹log ¹⁄_x = p
   ⇒ ⁸¹log ¹⁄_x = -1
   ⇒ ⁸¹log x^-1 = ⁸¹log (81)^-1
   ⇒ x^-1 = (81)^-1
   ⇒ x = 81
   
   Menentukan nilai y :
   ⇒ ^ylog ¹⁄₈₁ = p
   ⇒ ^ylog ¹⁄₈₁ = -1
   ⇒ ^ylog (81)^-1 = ^ylog y^-1
   ⇒ (81)^-1 = y^-1
   ⇒ y = 81
   
   Dengan demikian, kita peroleh :
   ⇒ 2x - 3y = 2(81) - 3(81)
   ⇒ 2x - 3y = 162 - 243
   ⇒ 2x - 3y = -81
   

   Jawaban : B

Share ke Facebook >>

Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.