Kuantor universal atau kuantor umum adalah pengungkapan yang menyatakan keseluruhan dan biasanya dinyatakan dengan kata semua atau setiap. Kata semua dan setiap disebut sebagai kuantor universal yang menunjukkan bahwa semua anggota memiliki kondisi atau karakter yang sama. Sesuai dengan namanya, kuantor eksistensial atau kuantor khusus adalah pengungkapan yang menunjukkan keberadaan khusus dan biasanya dinyatakan dengan kata beberapa atau ada. Kata ada dan beberapa disebut sebagai kuantor eksistensial yang menunjukkan beberapa atau ada anggota yang memiliki kondisi atau karakter tertentu yang berbeda dari umumnya. Pada kesempatan ini, Bahan belajar sekolah akan membahas beberapa pernyataan berkuantor universal dan pernyataan berkuantor eksistensial.
Kata semua atau setiap menunjukkan bahwa suatu kondisi berlaku untuk semua anggota atau berlaku keseragaman. Notasi dari suatu peryataan berkuantor umum ditulis dengan '∀x, p(x)' dan dibaca untuk setiap x belakulah p(x).
Untuk memahami pernyataan berkuantor universal, kita dapat memanfaatkan pendekatan himpunan. Misal diketahui beberapa himpunan sebagai berikut:
U = himpunan semua bilangan
A = himpunan semua bilangan prima
B = himpunan semua bilangan asli
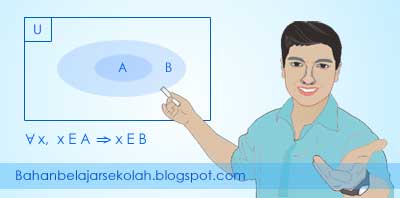
Jika digambarkan dalam bentuk diagram Venn, maka himpunan A, B, dan U akan terlihat seperti gambar di bawah ini. Perhatikan gambar dan lihat bahwa himpunan A berada di dalam himpunan B.
Dari diagram di atas dapat kita lihat bahwa himpunan A adalah bagian dari himpunan B. Dengan demikian, untuk semua x yang merupakan anggota A maka x juga anggota B. Hubungan ini dapat ditulis dengan notasi sebagai berikut:
Notasi di atas dapat dibaca "Jika x adalah anggota A, maka x adalah anggota B". Nah jika kita hubungkan ke himpunan awal, maka notasi di atas dapat dibaca "Jika x adalah bilangan prima, maka x adalah bilangan asli".
Berdasarkan pendekatan himpunan di atas, maka dapat disimpulkan bahwa pernyataan berkuantor universal "Semua A adalah B" ekuivalen dengan pernyataan implikasi "Jika x anggota A, maka x anggota B".
Contoh :
Tentukan implikasi yang ekuivalen dengan pernyataan berkuantor universal berikut:
a). Semua hewan herbivora memakan tumbuhan
b). Semua bintang K-pop pandai menari
c). Semua artis India berhidung mancung
d). Semua bilangan prima adalah bilangan asli
e). Semua segitiga sama sisi sama adalah segitiga sama kaki.
Jawaban :
Implikasi yang ekuivalen dengan kelima pernyataan tersebut adalah:
a). Jika kambing memakan tumbuhan, maka kambing hewan herbivora
b). Jika Yoona adalah bintang K-pop, maka ia pandai menari
c). Jika Kareena adalah artis India, maka ia berhidung mancung
d). Jika 3 adalah bilangan prima, maka 3 adalah bilangan asli
e). Jika segitiga ABC sama sisi, maka segitiga ABC sama kaki.
Baca juga : Hukum Ekuivalen dan Sifat-sifat Pernyataan Ekuivalen.
Kata ada atau beberapa menunjukkan bahwa suatu kondisi tidak berlaku untuk semua anggota atau terdapat variasi. Notasi dari suatu peryataan berkuantor khusus ditulis dengan 'Ǝx, p(x)' dan dibaca ada x yang berlaku p(x).
Jika dihubungkan dengan pendekatan himpunan, maka pernyataan berkuantor eksistensial menunjukkan bahwa bahwa ada sekurang-kurangnya satu elemen himpunan suatu himpunan yang juga merupakan anggota himpunan lain.
Dengan demikian, dapat disimpulkan bahwa pernyataan berkuantor eksistensial "Beberapa A adalah B" ekuivalen dengan pernyataan "Sekurang-kurangnya ada sebuah x anggota A yang merupakan anggota B".
Contoh :
Tentukan pernyataan yang ekuivalen dengan pernyataan berkuantor khusus berikut:
a). Beberapa hewan adalah pemakan tumbuhan
b). Beberapa penyanyi tidak pandai menyanyi
c). Beberapa bilangan genap adalah bilangan prima
d). Beberapa pemerintah daerah bersifat tidak jujur
e). Beberapa persamaan kuadrat memiliki akar kembar
Jawaban :
Pernyataan yang ekuivalen dengan kelima pernyataan tersebut adalah:
a). Sekurang-kurangnya ada seekor hewan yang pemakan tumbuhan
b). Sekurang-kurangnya ada seorang penyanyi yang tidak pandai menyanyi
c). Sekurang-kurangnya ada satu bilangan genap yang merupakan bilangan prima
d). Sekurang-kurangnya ada seorang pemerintah daerah yang bersifat tidak jujur
e). Sekurang-kurangnya ada sebuah persamaan kuadrat yang memiliki akar kembar.
Baca juga : Hubungan Implikasi, Konvers, Invers, dan Kontraposisi.
Pernyataan Berkuantor Universal
Pernyataan berkuantor universal adalah pernyataan yang menggunakan kuantor umum seperti semua, setiap, atau seluruh. Pernyataan berkuantor umum menggunakan notasi khusus berupa '∀' yang dibaca untuk semua atau untuk setiap.Kata semua atau setiap menunjukkan bahwa suatu kondisi berlaku untuk semua anggota atau berlaku keseragaman. Notasi dari suatu peryataan berkuantor umum ditulis dengan '∀x, p(x)' dan dibaca untuk setiap x belakulah p(x).
Untuk memahami pernyataan berkuantor universal, kita dapat memanfaatkan pendekatan himpunan. Misal diketahui beberapa himpunan sebagai berikut:
U = himpunan semua bilangan
A = himpunan semua bilangan prima
B = himpunan semua bilangan asli
Jika digambarkan dalam bentuk diagram Venn, maka himpunan A, B, dan U akan terlihat seperti gambar di bawah ini. Perhatikan gambar dan lihat bahwa himpunan A berada di dalam himpunan B.
Dari diagram di atas dapat kita lihat bahwa himpunan A adalah bagian dari himpunan B. Dengan demikian, untuk semua x yang merupakan anggota A maka x juga anggota B. Hubungan ini dapat ditulis dengan notasi sebagai berikut:
| ∀x, x E A ⇒ x E B |
Notasi di atas dapat dibaca "Jika x adalah anggota A, maka x adalah anggota B". Nah jika kita hubungkan ke himpunan awal, maka notasi di atas dapat dibaca "Jika x adalah bilangan prima, maka x adalah bilangan asli".
Berdasarkan pendekatan himpunan di atas, maka dapat disimpulkan bahwa pernyataan berkuantor universal "Semua A adalah B" ekuivalen dengan pernyataan implikasi "Jika x anggota A, maka x anggota B".
Contoh :
Tentukan implikasi yang ekuivalen dengan pernyataan berkuantor universal berikut:
a). Semua hewan herbivora memakan tumbuhan
b). Semua bintang K-pop pandai menari
c). Semua artis India berhidung mancung
d). Semua bilangan prima adalah bilangan asli
e). Semua segitiga sama sisi sama adalah segitiga sama kaki.
Jawaban :
Implikasi yang ekuivalen dengan kelima pernyataan tersebut adalah:
a). Jika kambing memakan tumbuhan, maka kambing hewan herbivora
b). Jika Yoona adalah bintang K-pop, maka ia pandai menari
c). Jika Kareena adalah artis India, maka ia berhidung mancung
d). Jika 3 adalah bilangan prima, maka 3 adalah bilangan asli
e). Jika segitiga ABC sama sisi, maka segitiga ABC sama kaki.
Baca juga : Hukum Ekuivalen dan Sifat-sifat Pernyataan Ekuivalen.
Pernyataan Berkuantor Eksistensial
Pernyataan berkuantor eksistensial adalah pernyataan yang menggunakan kuantor khusus seperti beberapa, ada, atau terdapat. Pernyataan berkuantor eksistensial menggunakan notasi khusus berupa 'Ǝ' yang dibaca untuk ada, beberapa, atau terdapat.Kata ada atau beberapa menunjukkan bahwa suatu kondisi tidak berlaku untuk semua anggota atau terdapat variasi. Notasi dari suatu peryataan berkuantor khusus ditulis dengan 'Ǝx, p(x)' dan dibaca ada x yang berlaku p(x).
Jika dihubungkan dengan pendekatan himpunan, maka pernyataan berkuantor eksistensial menunjukkan bahwa bahwa ada sekurang-kurangnya satu elemen himpunan suatu himpunan yang juga merupakan anggota himpunan lain.
Dengan demikian, dapat disimpulkan bahwa pernyataan berkuantor eksistensial "Beberapa A adalah B" ekuivalen dengan pernyataan "Sekurang-kurangnya ada sebuah x anggota A yang merupakan anggota B".
Contoh :
Tentukan pernyataan yang ekuivalen dengan pernyataan berkuantor khusus berikut:
a). Beberapa hewan adalah pemakan tumbuhan
b). Beberapa penyanyi tidak pandai menyanyi
c). Beberapa bilangan genap adalah bilangan prima
d). Beberapa pemerintah daerah bersifat tidak jujur
e). Beberapa persamaan kuadrat memiliki akar kembar
Jawaban :
Pernyataan yang ekuivalen dengan kelima pernyataan tersebut adalah:
a). Sekurang-kurangnya ada seekor hewan yang pemakan tumbuhan
b). Sekurang-kurangnya ada seorang penyanyi yang tidak pandai menyanyi
c). Sekurang-kurangnya ada satu bilangan genap yang merupakan bilangan prima
d). Sekurang-kurangnya ada seorang pemerintah daerah yang bersifat tidak jujur
e). Sekurang-kurangnya ada sebuah persamaan kuadrat yang memiliki akar kembar.
Baca juga : Hubungan Implikasi, Konvers, Invers, dan Kontraposisi.
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.