MENYUSUN SISTEM PERTIDAKSAMAAN LINEAR BILA GRAFIK DIKETAHUI

Untuk menyusun sistem pertidaksamaan linear bila grafik diketahui, kita diharuskan untuk jeli dalam menentukan tanda pertidaksamaan yang sesuai dengan grafik tersebut. Tanda tersebut dapat berupa kurang dari (<), kurang dari sama dengan (≤), lebih dari (>), ataupun lebih dari sama dengan (≥). Untuk mempermudah pemahaman, berikut disajikan ilustrasi tentang daerah himpunan penyelesaian berdasarkan tanda pertidaksamaan.

Menyusun Sistem Pertidaksamaan Linear

Bila himpunan penyelesaian suatu sistem pertidaksamaan linear telah disajikan dalam bentuk grafik, maka kita dapat menyusun sistem pertidaksamaan linear yang sesuai dengan grafik tersebut. Langkah pertama yang harus dilakukan adalah dengan melihat titik potong garis-garis pada grafik terhadap sumbu x dan sumbu y.

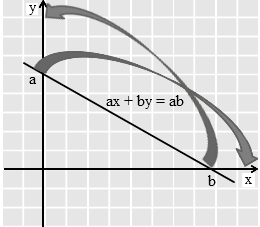
Kemudian dari titik koordinat tersebut kita susun persamaan garisnya dengan menggunakan rumus ax + by = ab seperti gambar ilustrasi di bawah ini. Selanjutnya, sistem pertidaksamaan yang bersesuaian dapat ditentukan dengan melihat daerah himpunan penyelesaian yang ditunjukkan dalam grafik. 

Untuk lebih jelasnya, lihat contoh di bawah ini :

1. Tentukan sistem pertidaksamaan yang memiliki daerah himpunan penyelesaian seperti gambar di bawah ini.
   
   
   
   
   Pembahasan :
   Dari grafik jelas terlihat ada 3 garis lurus yaitu :
   Untuk a = 6, b = 3
   persamaan garisnya 6x + 3y= 18 → 2x + y = 6
   
   Untuk a = 4, b = 6
   persamaan garisnya 4x + 6y = 24 → 2x + 3y = 12
   
   Untuk a = 2, b = tak hingga → y = 2
   
   Setelah persamaan garis diketahui, selanjutnya lihat daerah himpunan penyelesaian pada grafik (daerah yang diarsir/ berwarna gelap) kemudian tentukan hubungan pertidaksamaannya. Dari grafik jelas terlihat bahwa daerah himpunan penyelesaiannya memiliki 4 titik pojok, dengan begitu berarti ada 4 garis pembatas (kendala), yaitu :
   

   1. Di atas sumbu x → y ≥ 0
   2. Di atas (kanan) 2x + y = 6 → 2x + y ≥ 6
   3. Di bawah garis y = 2 → y ≤ 2
   4. Di bawah (kiri)  2x + 3y = 12 → 2x + 3y ≤ 12
    

   Jadi sistem pertidaksamaan yang memiliki daerah himpunan penyelesaian seperti gambar pada soal adalah 2x + y ≥ 6, 2x + 3y ≤ 12, dan 0 ≤ y ≤ 2.
   
   
   
2. Tentukan sistem pertidaksamaan yang memiliki daerah himpunan penyelesaian seperti gambar di bawah ini.
   
   
   
   
   Pembahasan :
   Dari grafik jelas terlihat ada 2 garis lurus yaitu :
   Untuk a = 4, b = 6
   persamaan garisnya 4x + 6y= 24 → 2x + 3y = 12
   
   Untuk a = tak hingga, b = 3 → x = 3
   
   Setelah persamaan garis diketahui, selanjutnya lihat daerah himpunan penyelesaian pada grafik kemudian tentukan hubungan pertidaksamaannya. Dari grafik jelas terlihat bahwa daerah himpunan penyelesaiannya memiliki 3 titik pojok, dengan begitu berarti ada 3 garis kendala, yaitu :
   

   1. Di atas sumbu x → y ≥ 0
   2. Di kanan x = 3 → x ≥ 3
   3. Di bawah garis 2x + 3y = 12 → 2x + 3y ≤ 12

   
   Jadi sistem pertidaksamaan yang memiliki daerah himpunan penyelesaian seperti gambar pada soal adalah y ≥ 0, x ≥ 3, 2x + 3y ≤ 12.
   
   

Share ke Facebook >>

Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.