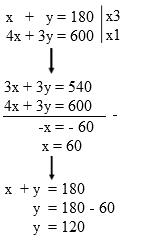Edutafsi.com - (Contoh 6 :
). Seorang pedagang buah hendak menjual buah mangga dan pisang dengan menggunakan
gerobak. Pedagang tersebut membeli buah mangga dengan harga Rp 8.000,00/kg
dan membeli buah pisang dengan harga Rp 6.000,00/kg. Modal yang tersedia Rp 1.200.000,00 dan
gerobaknya hanya dapat menampung mangga dan pisang sebanyak 180 kg. Jika
harga jual mangga adalah Rp 9.200,00/kg dan harga jual pisang adalah Rp 7.000,00/kg, maka
tentukanlah laba maksimum yang diperoleh pedagang tersebut!
Contoh Terkait : Menentukan Syarat Nilai Optimum Fungsi Tujuan
Sebuah perusahaan properti memproduksi dua macam lemari pakaian yaitu tipe lux dan tipe sport dengan menggunakan 2 bahan dasar yang sama yaitu kayu jati dan cat pernis. Untuk memproduksi 1 unit tipe lux dibutuhkan 10 batang kayu jati dan 3 kaleng cat pernis, sedangkan untuk memproduksi 1 unit tipe sport dibutuhkan 6 batang kayu jati dan 1 kaleng cat pernis.
Biaya produksi tipe lux dan tipe sport masing-masing adalah Rp 40.000 dan Rp 28.000 per unit. Untuk satu periode produksi, perusahaan menggunakan paling sedikit 120 batang kayu jati dan 24 kaleng cat pernis. Bila perusahaan harus memproduksi lemari tipe lux paling sedikit 2 buah dan tipe sport paling sedikit 4 buah, tentukan banyak lemari tipe lux dan tipe sport yang harus diproduksi agar biaya produksinya minimum!
Baca juga : Pembahasan Titik Optimum Fungsi Tujuan >>
Pembahasan :
Karena ditanya laba maksimum, maka fungsi tujuannya berhubungan dengan keuntungan dari menjual buah mangga dan buah pisang perkilonya. Oleh karena itu, fungsi tujuan dapat dinyatakan dalam variabel jumlah pisang dan jumlah mangga.
Karena variabel dalam soal ini adalah banyak mangga dan pisang yang dijual, maka dapat dilakukan pemisalan variabel sebagai berikut:
1). Banyak mangga yang dijual = x
2). Banyak pisang yang dijual = y
Selanjutnya, untuk menyusun fungsi tujuannya kita juga harus mengetahui terlebih dahulu keuntungan dari masing-masing penjualan mangga dan pisang. Berikut untung penjualan :
1). Keuntungan menjual mangga = 9.200 - 8.000 = 1.200
2). Keuntungan menjual pisang = 7.000 - 6000 = 1.000
Jika dinyatakan dalam variabel x dan y, maka fungsi tujuannya adalah :F(x,y) = 1.200x + 1.000y
Arti dari fungsi tujuan tersebut adalah berapa nilai x (banyak mangga yang dijual) dan nilai y (banyak pisang yang dijual) agar diperoleh nilai F yang terbesar. Dengan kata lain, agar diperoleh keuntungan yang maksimal.
Model matematika atau sistem pertidaksamaan yang memenuhi soal tersebut adalah :
1). Jumlah mangga dan pisang tidak lebih dari 180 kg → x + y ≤ 180
2). 8.000x + 6.000y ≤ 1.200.000 → 4x + 3y ≤ 600
3). Banyak mangga tidak mungkin negatif → x ≥ 0
4). Banya pisang tidak mungkin negatif → y ≥ 0
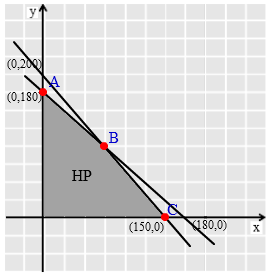
Titik potong masing-masing garis terhadap sumbu x dan sumbu y :
Garis x + y = 180
1). untuk x = 0 , maka y = 180 → titik potong (0, 180)
2). untuk y = 0, maka x = 180 → titik potong (180,0)
Garis 4x + 3y = 600
1). untuk x = 0, maka y = 200 → titik potong (0, 200)
2). untuk y = 0, maka x = 150 → titik potong (150, 0)
Selanjutnya gambarkan grafik yang bersesuain dengan sistem pertidaksamaan yang sudah diperoleh. Gunakan titik potong yang sudah dihitung di atas kemudian tentukan daerah himpunan penyelesaiannya. Daerah HP ditunjukkan oleh daerah yang diarsis pada gambar di bawah ini.
Dari grafik di atas diketahui ada tiga titik pojok yaitu A, B, dan C. Titik A dan C dapat ditentukan hanya dengan melihat gambar sedangkan titik B harus dihitung terlebih dahulu.
Titik B merupakan perpotongan antara garis x + y = 180 dengan 4x + 3y = 600.
Dari perhitungan tersebut, maka diketahui titik B(60, 120). Selanjutnya untuk dilakukan pengujian terhadap ketiag titik pojok A, B, dan C untuk mengetahui titik mana yang menghasilkan nilai F maksimum atau nilai terbesar.
Substitusi titik pojok pada fungsi objektif F(x,y) 1.200x + 1.000y :
1). A (0, 180) → F(x,y) =1.000(180) = 180.000
2). B (60, 120) → F(x,y) = 1.200(60) + 1.000(120) = 192.000
3). C (150,0) → F(x,y) = 1.200(150) = 180.000
Dari perhitungan di atas dapat dilihat bahwa titik yang menghasilan nilai terbesar adalah titik B(60, 120). Jadi laba maksimum yang diperoleh pedagang buah adalah Rp 192.000,00. Agar keuntungan maksimum, pedagang harus menjual 60 kg mangga dan 120 kg pisang.
Karena ditanya laba maksimum, maka fungsi tujuannya berhubungan dengan keuntungan dari menjual buah mangga dan buah pisang perkilonya. Oleh karena itu, fungsi tujuan dapat dinyatakan dalam variabel jumlah pisang dan jumlah mangga.
Karena variabel dalam soal ini adalah banyak mangga dan pisang yang dijual, maka dapat dilakukan pemisalan variabel sebagai berikut:
1). Banyak mangga yang dijual = x
2). Banyak pisang yang dijual = y
Selanjutnya, untuk menyusun fungsi tujuannya kita juga harus mengetahui terlebih dahulu keuntungan dari masing-masing penjualan mangga dan pisang. Berikut untung penjualan :
1). Keuntungan menjual mangga = 9.200 - 8.000 = 1.200
2). Keuntungan menjual pisang = 7.000 - 6000 = 1.000
Jika dinyatakan dalam variabel x dan y, maka fungsi tujuannya adalah :F(x,y) = 1.200x + 1.000y
Arti dari fungsi tujuan tersebut adalah berapa nilai x (banyak mangga yang dijual) dan nilai y (banyak pisang yang dijual) agar diperoleh nilai F yang terbesar. Dengan kata lain, agar diperoleh keuntungan yang maksimal.
Model matematika atau sistem pertidaksamaan yang memenuhi soal tersebut adalah :
1). Jumlah mangga dan pisang tidak lebih dari 180 kg → x + y ≤ 180
2). 8.000x + 6.000y ≤ 1.200.000 → 4x + 3y ≤ 600
3). Banyak mangga tidak mungkin negatif → x ≥ 0
4). Banya pisang tidak mungkin negatif → y ≥ 0
Titik potong masing-masing garis terhadap sumbu x dan sumbu y :
Garis x + y = 180
1). untuk x = 0 , maka y = 180 → titik potong (0, 180)
2). untuk y = 0, maka x = 180 → titik potong (180,0)
Garis 4x + 3y = 600
1). untuk x = 0, maka y = 200 → titik potong (0, 200)
2). untuk y = 0, maka x = 150 → titik potong (150, 0)
Selanjutnya gambarkan grafik yang bersesuain dengan sistem pertidaksamaan yang sudah diperoleh. Gunakan titik potong yang sudah dihitung di atas kemudian tentukan daerah himpunan penyelesaiannya. Daerah HP ditunjukkan oleh daerah yang diarsis pada gambar di bawah ini.
Dari grafik di atas diketahui ada tiga titik pojok yaitu A, B, dan C. Titik A dan C dapat ditentukan hanya dengan melihat gambar sedangkan titik B harus dihitung terlebih dahulu.
Titik B merupakan perpotongan antara garis x + y = 180 dengan 4x + 3y = 600.
Substitusi titik pojok pada fungsi objektif F(x,y) 1.200x + 1.000y :
1). A (0, 180) → F(x,y) =1.000(180) = 180.000
2). B (60, 120) → F(x,y) = 1.200(60) + 1.000(120) = 192.000
3). C (150,0) → F(x,y) = 1.200(150) = 180.000
Dari perhitungan di atas dapat dilihat bahwa titik yang menghasilan nilai terbesar adalah titik B(60, 120). Jadi laba maksimum yang diperoleh pedagang buah adalah Rp 192.000,00. Agar keuntungan maksimum, pedagang harus menjual 60 kg mangga dan 120 kg pisang.
Contoh Terkait : Menentukan Syarat Nilai Optimum Fungsi Tujuan
Biaya produksi tipe lux dan tipe sport masing-masing adalah Rp 40.000 dan Rp 28.000 per unit. Untuk satu periode produksi, perusahaan menggunakan paling sedikit 120 batang kayu jati dan 24 kaleng cat pernis. Bila perusahaan harus memproduksi lemari tipe lux paling sedikit 2 buah dan tipe sport paling sedikit 4 buah, tentukan banyak lemari tipe lux dan tipe sport yang harus diproduksi agar biaya produksinya minimum!
Baca juga : Pembahasan Titik Optimum Fungsi Tujuan >>
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.