MENENTUKAN NILAI MAKSIMUM FUNGSI TUJUAN DENGAN GARIS SELIDIK

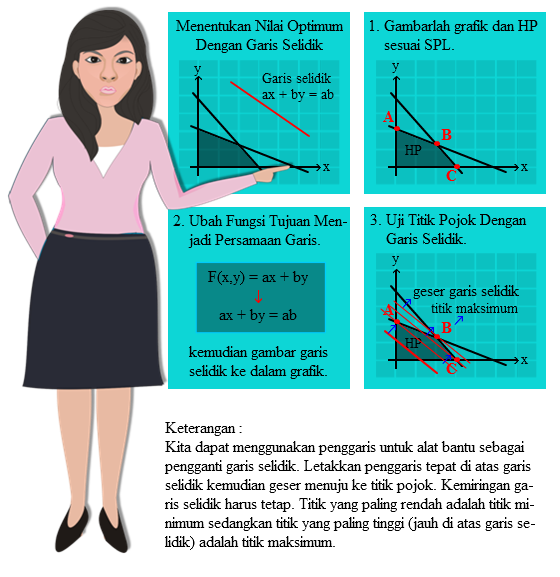
Garis selidik merupakan garis yang dibentuk dari fungsi tujuan untuk menyelidiki titik mana pada daerah himpunan penyelesaian yang akan menghasilkan nilai maksimum jika disubstitusikan ke fungsi tujuan. Jika diberikan fungsi tujuan f(x,y) = ax + by, maka kita dapat membuat garis selidik dengan rumus ax + by = ab.

Pada dasarnya garis selidik ini berfungsi untuk melihat titik mana yang paling tinggi berdasarkan kemiringan garis selidik. Titik yang paling dekat dengan garis selidik merupakan titik minimum yang akan menghasilkan nilai minimum sedangkan titik yang paling jauh dengan garis selidik akan menghasilkan nilai maksimum.

Keuntungan menggunakan garis selidik dalam menentukan nilai maksimum fungsi tujuan adalah kita tidak perlu mensubstitusikan tiap-tiap titik ke fungsi tujuan untuk mencari nilai mana yang maksimum.

Dengan garis selidik, kita cukup mencari 1 titik yang paling tinggi kemudian kita substitusikan ke persamaan fungsi tujuan untuk mengetahui nilai maksimumnya.

Contoh Soal :

Daerah yang diarsir pada gambar di bawah ini merupakan himpunan penyelesaian suatu sistem pertidaksamaan linear. Tentukan ilai maksimum dari fungsi tujuan 2x + 5y dengan menggunakan garis selidik.

Pembahasan :
Fungsi tujuan 2x + 5y maka garis selidiknya adalah 2x + 5y = 10. Titik potong garis selidik terhadap sumbu x dan sumbu y adalah :
untuk x = 0 maka y = 2 ---> (0,2)
untuk y = 0 maka x = 5 ---> (5,0)

Selanjutnya tarik garis lurus yang menghubungkan kedua titik potong tersebut sehingga dihasilkan gambar seperti berikut :

Untuk melihat titik aman yang paling jauh dari garis selidik, kita dapat menggunakan penggrais. Letakkan penggaris tepat di atas garis selidik kemudian geser penggaris ke atas dan tetap jaga agar kemiringannya tidak berubah. Titik yang terakhir menyentuh penggaris adalah titik nilai maksimum.

Dari tiga titik yang berada di atas garis selidik, titik B merupakan titik terjauh atau tertinggi. Oleh karena itu titik B merupakan titik yang kita cari agar nilai fungsi tujuannya maksimum. Titik B merupakan perpotongan antara dua garis yaitu garis y = 2 dan garis yang belum kita ketahui persamaannya. Untuk itu kita tentukan dulu persamaan garis yang berpotongan di titik B dengan skema dan rumus berikut :

Untuk a = 4 dan b = 6
persamaan garisnya 4x + 6y = 24 ---> 2x + 3y = 12

Titik potong garis y = 2 dan 2x + 3y = 12 dapat ditentukan dengan mensubstitusikan nilai y = 2 ke persamaan garis 2x + 3y = 12.

2x + 3(2) = 12

2x = 12 - 6 = 6 maka x = 3 dengan begitu titik B (3,2)

Maka nilai maksimumnya adalalah :
f(x,y) = 2x + 5y = 2(3) + 5(2) = 16
Daerah yang diarsir pada gambar di bawah ini merupakan himpunan penyelesaian suatu sistem pertidaksamaan linear. Tentukan ilai maksimum dari f(x,y) = x + 2y dengan menggunakan garis selidik.

Pembahasan :
Fungsi tujuan x + 2y maka garis selidiknya x + 2y = 2.

Berdasarkan garis selidik, maka titik (0,4) merupakan titik yang menghasilkan nilai maksimum.
f (x,y) = x + 2y = 0 + 2(4) = 8