Selain pertidaksamaan linear satu variabel, pertidaksamaan juga dapat dinyatakan dalam bentuk pecahan dan biasa disebut sebagai pertidaksamaan pecahan. Pertidaksamaan satu variabel berbentuk pecahan adalah bentuk pertidaksamaan yang memiliki dua bagian, yaitu bagian pembilang dan bagian penyebut. Pertidaksamaan pecahan ditandai dengan adanya bagian penyebut dan adanya sebuah variabel atau peubah pada bagian penyebutnya. Sama seperti pertidaksamaan linear satu variabel, pertidaksamaan berbentuk pecahan juga dapat diselesaikan dengan menggunakan garis bilangan. Garis bilangan digunakan untuk menggambarkan interval berdasarkan nilai yang menyebabkan bagian penyebut dan bagian pembilang bernilai nol. Himpunan penyelesaiannya kemudian ditentukan dengan menggunakan bantuan nilai uji. Pada kesempatan ini, Bahan belajar sekolah akan memaparkan bentuk umum dan penyelesaian pertidaksamaan pecahan.
Misal bagian pembilang adalah f(x) dan bagian penyebut adalah g(x), maka bentuk baku dari pertidaksamaan pecahan dalam variabel x dapat dinyatakan menjadi empat macam, yaitu:
a). Pertidaksamaan kurang dari : f(x)/g(x) < 0
b). Pertidaksamaan lebih dari : f(x)/g(x) > 0
c). Pertidaksamaan kurang dari sama dengan : f(x)/g(x) ≤ 0
d). Pertidaksamaan lebih dari sama dengan : f(x)/g(x) ≥ 0.
Perbedaan dari keempat macam bentuk baku pertidaksamaan pecahan di atas hanya terletak pada tanda pertidaksamaannya saja. Akan tetapi, tentu saja tanda pertidaksamaan yang digunakan akan sangat mempengaruhi penyelesaiannya nanti.
Contoh pertidaksamaan percahan:
1). (x - 3)/(2x + 4) < 0
2). 3/(2x + 4) > 0
3). (x - 1)/(x - 5) ≤ 0
4). (x2 - 4)/(x2 - 4x + 4) ≥ 0
Selain dari segi tanda pertidaksamaannya, perbedaan antara keempat macam bentuk baku di atas terletak pada penggambaran interval di garis bilangan. Perbedaan tersebut menimbulkan istilah interval tertutup dan interval terbuka.
Interval terbuka ditandai dengan penggunaan lingkaran atau bulatan kosong (lingkaran putih) tepat di atas bilangan ujung (bilangan yang menyebabkan persamaan bernilai nol). Sedangkan interval tertutup ditandai dengan penggunaan lingkaran berisi atau bulatan tertutup (lingkaran berwarna).
Perhatikan gambar di atas. Bulatan kosong menandakan bahwa a dan b tidak termasuk ke dalam interval atau himpunan penyelesaian. Sedangkan bulatan terutup menandakan bahwa nilai a dan b termasuk himpunan penyelesaian.
Intervak terbuka dan tertutup menjadi salah satu pembeda antara pertidaksamaan. Interval terbuka digunakan untuk menyatakan penyelesaian pertidaksamaan kurang dari (<) dan lebih dari (>). Interval tertutup digunakan untuk menyatakan penyelesaian pertidaksamaan kurang dari sama dengan (≤) dan lebih dari sama dengan (≥).
Baca juga : Himpunan Penyelesaian Pertidaksamaan Linear Satu Variabel.
Nilai-nilai uji tersebut selanjutnya disubstitusikan ke pertidaksamaan dan dilihat hasilnya. Dari hasil yang diperoleh selanjutnya dilihat nilai uji mana atau interval mana yang memenuhi pertidaksamaan dan merupakan himpunan penyelesaiannya.
Berdasarkan uraian tersebut, secara umum pertidaksamaan percahan dapat diselesaikan dengan beberapa langkah sebagai berikut:
1. Tentukan nilai nol untuk bagian pembilang dan penyebut
2. Gambarkan nilai-nilai nol tersebut ke garis bilangan
3. Ambil nilai uji yang mewakili masing-masing interval
4. Susbtitusi nilai uji untu melihat tanda interval
5. Simpulkan himpunan penyelesaian berdasarkan tanda-tanda interval yang diperoleh.
Contoh soal :
Tentukan himpunan penyelesaian untuk pertidaksamaan pecahan berikut:
Pembahasan :
Langkah pertama, kita tentukan nilai-nilai nol untuk bagian pembilang dan bagian penyebut. Pada pertidaksamaan di atas, bagian pembilang adalah 2x + 4 dan bagian penyebut adalah 3x - 6.
Nilai nol untuk bagian pembilang:
⇒ 2x + 4 = 0
⇒ 2x = -4
⇒ x = -2
Nilai nol untuk bagian penyebut:
⇒ 3x - 6 = 0
⇒ 3x = 6
⇒ x = 2
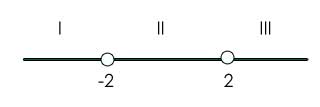
Langkah kedua, kita gambar nilai x pembuat nol ke dalam garis bilangan sebagai berikut:
Dari gambar garis bilangan tersebut kita peroleh tiga interval, yaitu:
1). Interval sebelah kiri : x < -2
2). Interval bagian tengah : -2 < x < 2
3). Interval sebelah kanan : x > 2
Langkah ketiga, kita ambil nilai uji untuk mewakili masing-masing interval misalnya sebagai berikut:
1). Nilai uji x = -3 untuk mewakili interval pertama
2). Nilai uji x = 0 untuk mewakili interval kedua
3). Nilai uji x = 3 untuk mewakili interval ketiga.
Langkah keempat, substitusikan ketiga nilai uji ke pertidaksamaan pecahan untuk melihat tanda-tanda intervalnya.
Langkah terakhir kita simpulkan himpunan penyelesaian pertidaksamaan berdasarkan tanda interval yang kita peroleh. Karena pertidaksamaan dalam soal menggunakan tanda kurang dari (<), maka nilai yang memenuhi adalah nilai yang menyebabkan hasilnya negatif atau < 0.
Itu artinya, dari ketiga nilai uji atau dari ketiga interval yang ada, nilai uji x = 0 lah yang memenuhi pertidaksamaan. Karena x = 0 mewakili interval -2 < x < 2, maka himpunan penyelesaian yang tepat untuk pertidaksamaan tersebut adalah HP = {x| -2 < x < 2}.
Baca juga : Kumpulan Soal dan Pembahasan Tentang Pertidaksamaan.
Bentuk Umum Pertidaksamaan Pecahan
Seperti yang dipaparkan di atas, pertidaksamaan berbentuk pecahan terdiri dari dua bagian yaitu bagian pembilang dan bagian penyebut dan menggunakan tanda pertidaksamaan untuk membedakan kedua ruasnya. Tanda pertidaksamaan tersebut antaralain kurang dari, lebih dari, kurang dari sama dengan, dan lebih dari sama dengan.Misal bagian pembilang adalah f(x) dan bagian penyebut adalah g(x), maka bentuk baku dari pertidaksamaan pecahan dalam variabel x dapat dinyatakan menjadi empat macam, yaitu:
a). Pertidaksamaan kurang dari : f(x)/g(x) < 0
b). Pertidaksamaan lebih dari : f(x)/g(x) > 0
c). Pertidaksamaan kurang dari sama dengan : f(x)/g(x) ≤ 0
d). Pertidaksamaan lebih dari sama dengan : f(x)/g(x) ≥ 0.
Perbedaan dari keempat macam bentuk baku pertidaksamaan pecahan di atas hanya terletak pada tanda pertidaksamaannya saja. Akan tetapi, tentu saja tanda pertidaksamaan yang digunakan akan sangat mempengaruhi penyelesaiannya nanti.
Contoh pertidaksamaan percahan:
1). (x - 3)/(2x + 4) < 0
2). 3/(2x + 4) > 0
3). (x - 1)/(x - 5) ≤ 0
4). (x2 - 4)/(x2 - 4x + 4) ≥ 0
Selain dari segi tanda pertidaksamaannya, perbedaan antara keempat macam bentuk baku di atas terletak pada penggambaran interval di garis bilangan. Perbedaan tersebut menimbulkan istilah interval tertutup dan interval terbuka.
Interval terbuka ditandai dengan penggunaan lingkaran atau bulatan kosong (lingkaran putih) tepat di atas bilangan ujung (bilangan yang menyebabkan persamaan bernilai nol). Sedangkan interval tertutup ditandai dengan penggunaan lingkaran berisi atau bulatan tertutup (lingkaran berwarna).
Perhatikan gambar di atas. Bulatan kosong menandakan bahwa a dan b tidak termasuk ke dalam interval atau himpunan penyelesaian. Sedangkan bulatan terutup menandakan bahwa nilai a dan b termasuk himpunan penyelesaian.
Intervak terbuka dan tertutup menjadi salah satu pembeda antara pertidaksamaan. Interval terbuka digunakan untuk menyatakan penyelesaian pertidaksamaan kurang dari (<) dan lebih dari (>). Interval tertutup digunakan untuk menyatakan penyelesaian pertidaksamaan kurang dari sama dengan (≤) dan lebih dari sama dengan (≥).
Baca juga : Himpunan Penyelesaian Pertidaksamaan Linear Satu Variabel.
Cara Menyelesaikan Pertidaksamaan Pecahan
Pertidaksamaan pecahan dapat diselesaikan dengan bantuan garis bilangan. Interval yang digambar dalam garis bilangan diperoleh melalui nilai nol untuk bagian pembilang dan nilai nol untuk bagian penyebut. Setelah dihasilkan tiga interval, selanjutnya diambil nilai uji untuk masing-masing interval.Nilai-nilai uji tersebut selanjutnya disubstitusikan ke pertidaksamaan dan dilihat hasilnya. Dari hasil yang diperoleh selanjutnya dilihat nilai uji mana atau interval mana yang memenuhi pertidaksamaan dan merupakan himpunan penyelesaiannya.
Berdasarkan uraian tersebut, secara umum pertidaksamaan percahan dapat diselesaikan dengan beberapa langkah sebagai berikut:
1. Tentukan nilai nol untuk bagian pembilang dan penyebut
2. Gambarkan nilai-nilai nol tersebut ke garis bilangan
3. Ambil nilai uji yang mewakili masing-masing interval
4. Susbtitusi nilai uji untu melihat tanda interval
5. Simpulkan himpunan penyelesaian berdasarkan tanda-tanda interval yang diperoleh.
Contoh soal :
Tentukan himpunan penyelesaian untuk pertidaksamaan pecahan berikut:
| 2x + 4 | < 0 |
| 3x - 6 |
Pembahasan :
Langkah pertama, kita tentukan nilai-nilai nol untuk bagian pembilang dan bagian penyebut. Pada pertidaksamaan di atas, bagian pembilang adalah 2x + 4 dan bagian penyebut adalah 3x - 6.
Nilai nol untuk bagian pembilang:
⇒ 2x + 4 = 0
⇒ 2x = -4
⇒ x = -2
Nilai nol untuk bagian penyebut:
⇒ 3x - 6 = 0
⇒ 3x = 6
⇒ x = 2
Langkah kedua, kita gambar nilai x pembuat nol ke dalam garis bilangan sebagai berikut:
Dari gambar garis bilangan tersebut kita peroleh tiga interval, yaitu:
1). Interval sebelah kiri : x < -2
2). Interval bagian tengah : -2 < x < 2
3). Interval sebelah kanan : x > 2
Langkah ketiga, kita ambil nilai uji untuk mewakili masing-masing interval misalnya sebagai berikut:
1). Nilai uji x = -3 untuk mewakili interval pertama
2). Nilai uji x = 0 untuk mewakili interval kedua
3). Nilai uji x = 3 untuk mewakili interval ketiga.
Langkah keempat, substitusikan ketiga nilai uji ke pertidaksamaan pecahan untuk melihat tanda-tanda intervalnya.
| Nilai uji | Substitusi | Tanda interval |
| x = -3 | {2(-3) + 4}/{3(-3) - 6} = 2/15 | Positif atau > 0 |
| x = 0 | {2(0) + 4}/{3(0) - 6} = 4/-6 | Negatif atau < 0 |
| x = 3 | {2(3) + 4}/{3(3) - 6} = 10/3 | Positif atau > 0 |
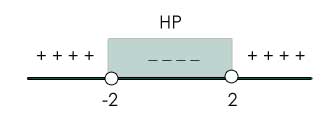
Langkah terakhir kita simpulkan himpunan penyelesaian pertidaksamaan berdasarkan tanda interval yang kita peroleh. Karena pertidaksamaan dalam soal menggunakan tanda kurang dari (<), maka nilai yang memenuhi adalah nilai yang menyebabkan hasilnya negatif atau < 0.
Itu artinya, dari ketiga nilai uji atau dari ketiga interval yang ada, nilai uji x = 0 lah yang memenuhi pertidaksamaan. Karena x = 0 mewakili interval -2 < x < 2, maka himpunan penyelesaian yang tepat untuk pertidaksamaan tersebut adalah HP = {x| -2 < x < 2}.
Baca juga : Kumpulan Soal dan Pembahasan Tentang Pertidaksamaan.
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.