Edutafsi.com - Besaran Vektor. Sebagian besar besaran turunan merupakan besaran vekor yaitu besaran yang memiliki nilai dan arah misalnya kecepatan, gaya, perpindahan dan sebagainya. Besaran yang hanya memiliki nilai saja disebut besaran skalar misalnya massa, waktu, jarak, kelajuan, dan sebagainya. Jika berbicara mengenai besaran vektor, maka yang menjadi fokus kita adalah nilai dan arah. Analisis arah sangat menentukan hasil yang diperoleh dalam penentuan resultan atau penjumlahan beberapa vektor. Cara yang paling umum digunakan untuk menentukan resultan dua vektor adalah dengan aturan cosinus. Untuk vektor-vektor yang segaris, resultan vektornya dapat dihitung dengan cara menjumlahkan atau mengurangkan vektor-vektor tersebut secara aljabar biasa. Di bawah ini dibahas beberapa contoh.
Contoh 1 : Menentukan Besar Vektor
Dua buah vektor A dan B mengapit sudut 120o. Resultan kedua vektor adalah 20√3 N. Jika resultan tersebut membentuk sudut 30o terhadap vektor A, maka besar A dan B adalah .....
A. 20 N dan 40 N
B. 40 N dan 20 N
C. 20√3 N dan 40√3 N
D. 40√3 N dan 20√3 N
E. 20√3 N dan 20√3 N
Pembahasan :
Jika digambarkan akan terlihat seperti di gambar di bawah ini :
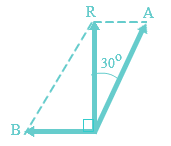
Berdasarkan aturan sinus, maka berlaku :
| A | = | B | = | R |
| sin 90 | sin 30 | sin 120 |
| A | = | R |
| sin 90 | sin 120 |
| A | = | 20√3 |
| 1 | (-½) |
Besar vektor B dapat dihitung dengan persamaan :
| A | = | R |
| sin 90 | sin 120 |
| A | = | 20√3 |
| 1 | (-½) |
⇒ T2 = 500 N
Jadi, T1 = T2 = 500 N.
Jawaban : C
Sebuah perahu menyeberangi sungai yang lebarnya 100 m dengan kelajuan 4 m/s tegak lurus terhadap arah arus sungai. Jika air sungai mengalir dengan kecepatan 3 m/s, maka jarak tempuh perahu tersebut sampai di seberang sungai adalah .....
A. 100 m
B. 105 m
C. 110 m
D. 115 m
E. 125 m
Pembahasan :
Dik : Vair = Va = 3m/s, Vperahu = Vp = 4 m/s, x = 100 m.
Karena perahu bergerak tegak lurus arah aliran sungai, maka sudut antara Va dan Vp adalah 90o. Dengan begitu kecepatan resultannya dapat dihitung dengan menggunakan dalil Phytagoras sebagai berikut :
⇒ Vr = √Va2 + Vp2
⇒ Vr = √32 + 42
⇒ Vr = 5 m/s.
Sudut yang dibentuk resultan dengan vektor kecepatan air adalah :
| ⇒ sin a = | Vp |
| Vr |
| ⇒ sin a = | 4 |
| 5 |
Dengan demikian, jarak yang ditempuh oleh perahu (s) adalah :
| ⇒ sin 53o = | x |
| s |
| ⇒ | 4 | = | 100 |
| 5 | s |
Jawaban : E.
Contoh 3 : Aturan Cosinus
Dua buah vektor gaya P dan R mengapit sudut 53o dan menghasilkan resultan sebesar 40√2 N. Jika P : R = 1 : 5, maka besar vektor P dan Q adalah .....
A. 6 N dan 6 N
B. 2 N dan 10 N
C. 10 N dan 2 N
D. 8 N dan 4 N
E. 4 N dan 8 N
Pembahasan :
Dik : R = 15 N, P/R = 1/5, maka R = 5P
Berdasarkan aturan cosinus :
⇒ R = √P2 + R2 + 2PR cos θ
⇒ R = √P2 + (5P)2 + 2P(5P) cos 53o
⇒ R = √P2 + 25P2 + 10P2 (⅗)
⇒ R = √32P2
⇒ R = √(16 x 2)P2
⇒ 40√2 = 4P√2
⇒ P = 10N
Dengan demikian, besar vektor Q adalah :
⇒ Q = ⅕ P
⇒ Q = ⅕ (10)⇒ Q = 2 N
Jawaban : C
Contoh 4 : Resultan Vektor
A. 18 N
B. 20 N
C. 22 N
D. 24 N
E. 30 N
Pembahasan :
Dik : F2 = 15 N.
Berdasarkan aturan sinus :
| F2 | = | F1 | = | R |
| sin 30o | sin 37o | sin 67o |
| 15 | = | F1 |
| sin 30o | sin 37o |
| 15 | = | F1 |
| ½ | ⅗ |
Jawaban : A
Contoh 5 : Menentukan Resultan Vektor
A. 10 N
B. 20 N
C. 30 N
D. 40 N
E. 50 N
Pembahasan :
Diketahui : A = B = C = 15 N.
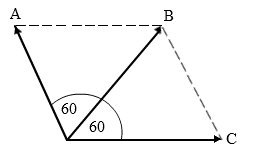
⇒ R = A + B + C
⇒ R = B + B
⇒ R = 2B
⇒ R = 2(15)
⇒ R = 30 N.
Jawaban di atas juga dapat dibuktikan dengan aturan cosinus. Sudut yang dibentuk oleh A dan C adalah 120o, sehingga :
⇒ A + C = √A2 + C2 + 2A.C cos θ
⇒ A + C = √A2 + A2 + 2A.A cos 120o
⇒ A + C = √2A2 + 2A2 (-½)
⇒ A + C = A
Karena A = B = C = 15 N, maka :
⇒ R = A + B + C
⇒ R = A + C + B
⇒ R = A + B
⇒ R = 15 N + 15 N
⇒ R = 30 N.
Jawaban : C
Edutafsi.com adalah blog tentang bahan belajar. Gunakan menu atau penelusuran untuk menemukan bahan belajar yang ingin dipelajari.